题目内容

设不等式组
x＞0
y＞0
y≤-nx+4n
(n∈N*)所表示的平面区域Dn的整点（即横坐标和纵坐标均为整数的点）个数为an，则
1
2010
(a2+a4+…+a2010)=
 
．
分析：利用不等式对应的图形为三角形，求出所有的整数点个数，判断出an为等差数列，利用等差数列的前n项和公式求出前n项和．
解答：解：
x＞0
y＞0
y≤-nx+4n
(n∈N*)所表示的平面区域Dn的整点个数
an=3n+2n+n=6n
∴{an}为等差数列
∴a2，a4，…a2010也为等差数列
∴
1
2010
(a2+a4+…+a2010)
=
1
2010
×
(a2+a2010)×1005
2

═
1
2010
×
(12 +2010×6 )×1005
2

=3018
故答案为3018．
点评：求数列的前n项和，首先要求出数列的通项，利用通项的特点选择合适的求和方法．
练习册系列答案
相关题目
设不等式组
|x|-2≤0
y-3≤0
x-2y≤2
所表示的平面区域为S，则S的面积为
 
；若A、B为S内的两个点，则|AB|的最大值为
 
．
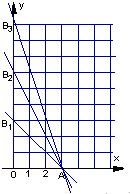精英家教网在平面直角坐标系上，设不等式组
x＞0
y＞0
y≤-m(x-3)
（n∈N*）
所表示的平面区域为Dn，记Dn内的整点（即横坐标和纵坐标均
为整数的点）的个数为an（n∈N*）．
（Ⅰ）求a1，a2，a3并猜想an的表达式再用数学归纳法加以证明；
（Ⅱ）设数列{an}的前项和为Sn，数列{
1
Sn
}的前项和Tn，
是否存在自然数m？使得对一切n∈N*，Tn＞m恒成立．若存在，
求出m的值，若不存在，请说明理由．
（2012•茂名二模）在平面直角坐标系上，设不等式组
x＞0
y≥0
y≤-2n(x-3)
（n∈N*）表示的平面区域为Dn，记Dn内的整点（横坐标和纵坐标均为整数的点）的个数为an．
（1）求出a1，a2，a3的值（不要求写过程）；
（2）证明数列{an}为等差数列；
（3）令bn=
1
anan+1
（n∈N*），求b1+b2+…+bn．
（2006•宣武区一模）设不等式组
x＞0
y＞0
y≤-nx+3n
所表示的平面区域为Dn，记Dn内的整点个数为an（n∈N*）．（整点即横坐标和纵坐标均为整数的点）
（Ⅰ）求数列{an}的通项公式；
（Ⅱ）记数列{an}的前n项和为Sn，且Tn=
Sn
3•2n-1
，若对于一切的正整数n，总有Tn≤m，求实数m的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网