题目内容
已知二次函数f(x)=x2-ax+a(x∈R)同时满足:
①不等式f(x)≤0的解集有且只有一个元素;
②在定义域内存在0<x1<x2,使得不等式f(x1)>f(x2)成立,设数列{an}的前n项和Sn=f(n).
(Ⅰ)求函数f(x)的表达式;
(Ⅱ)求数列{an}的通项公式;
(Ⅲ)设各项均不为0的数列{cn}中,所有满足ci·ci+1<0的整数i的个数称为这个数列{cn}的变号数,令![]() (n∈N*),求数列{cn}的变号数.
(n∈N*),求数列{cn}的变号数.
答案:
解析:
解析:
|
解:(Ⅰ)∵不等式 ∴ 当 当 综上得 (Ⅱ)由(Ⅰ)知 当 当 ∴ (Ⅲ)由题设可得 ∵ ∵当 即当 ∵ ∴数列{ |

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
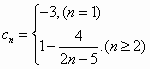 11分
11分