题目内容
设数列
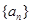 是以2为首项,1为公差的等差数列,
是以2为首项,1为公差的等差数列,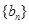 是以1为首项,2为公比的等比数列,则
是以1为首项,2为公比的等比数列,则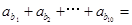 ( )
( )| A.1033 | B.1034 | C.2057 | D.2058 |
A
首先根据数列{an}是以2为首项,1为公差的等差数列,{bn}是以1为首项,2为公比的等比数列,求出等差数列和等比数列的通项公式,然后根据ab1+ab2+…+ab10=1++2+23+25+…+29+10进行求和.
解:∵数列{an}是以2为首项,1为公差的等差数列,
∴an=2+(n-1)×1=n+1,
∵{bn}是以1为首项,2为公比的等比数列,
∴bn=1×2n-1,
依题意有:ab1+ab2+…+ab10=1+2+22+23+25+…+29+10=1033,
故选A.
解:∵数列{an}是以2为首项,1为公差的等差数列,
∴an=2+(n-1)×1=n+1,
∵{bn}是以1为首项,2为公比的等比数列,
∴bn=1×2n-1,
依题意有:ab1+ab2+…+ab10=1+2+22+23+25+…+29+10=1033,
故选A.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目
 )
)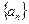 的公差为
的公差为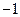 , 且
, 且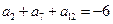 ,
,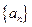 的通项公式
的通项公式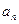 与前
与前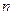 项和
项和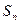 ;
; 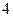 项抽去其中一项后,剩下三项按原来顺序恰为等比数列
项抽去其中一项后,剩下三项按原来顺序恰为等比数列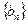
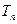 , 若存在
, 若存在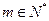 , 使对任意
, 使对任意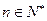 总有
总有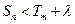 恒成立, 求实数
恒成立, 求实数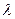 的取值范围.K
的取值范围.K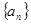 的公差为
的公差为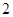 ,若
,若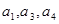 成等比数列, 则
成等比数列, 则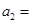 ( )
( )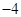



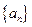 中,
中,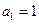 ,
,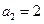 ,且
,且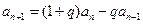
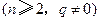 .
.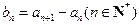 ,证明
,证明 是等比数列;
是等比数列;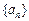 满足条件
满足条件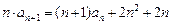 ,
, ,
,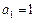 ,设
,设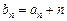

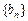 的通项公式;
的通项公式;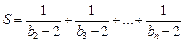 。(14分)
。(14分)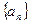 的各项都为正数,其前
的各项都为正数,其前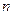 项和为
项和为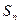 ,已知对任意
,已知对任意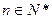 ,
,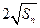 是
是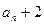 和
和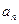 的等比中项.
的等比中项.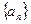 的通项公式;
的通项公式;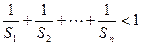 ;
;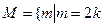 ,
,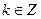 ,且
,且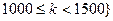 ,若存在
,若存在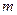 ∈
∈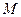 ,使对满足
,使对满足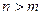 的一切正整数
的一切正整数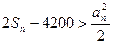 恒成立,求这样的正整数
恒成立,求这样的正整数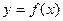 的图象经过坐标原点,与
的图象经过坐标原点,与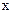 轴的另一个交点为
轴的另一个交点为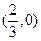 ,且
,且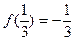 ,数列
,数列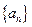 的前
的前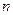 项的和为
项的和为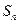 ,点
,点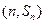 在函数
在函数 ,求数列
,求数列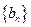 的前
的前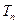 .
.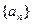 中,
中,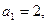 公积为5,当n为奇数时,这个数列的前
公积为5,当n为奇数时,这个数列的前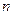 项和
项和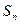 =_________。
=_________。
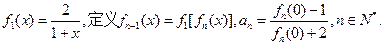
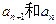 的递推关系式,并求出
的递推关系式,并求出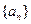 的通项公式;
的通项公式;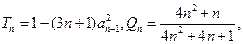 试比较
试比较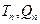 大小
大小 并证明
并证明