题目内容
已知复数z与(z+2)2-8i均是纯虚数,则z等于
- A.2i
- B.-2i
- C.i
- D.-i
B
试题分析:设z=bi(b∈R且b≠0),则(z+2)2-8i=(bi+2)2-8i=b2i2+4bi+4-8i=(4-b2)+(4b-8)i.
∴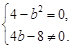 ∴
∴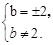
∴b=-2.∴z=-2i.故选B。
考点:本题考查复数的基本知识及四则运算.
点评:此类问题通常利用两复数相等的充要条件转化为实数问题去解。
试题分析:设z=bi(b∈R且b≠0),则(z+2)2-8i=(bi+2)2-8i=b2i2+4bi+4-8i=(4-b2)+(4b-8)i.
∴
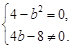 ∴
∴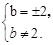
∴b=-2.∴z=-2i.故选B。
考点:本题考查复数的基本知识及四则运算.
点评:此类问题通常利用两复数相等的充要条件转化为实数问题去解。

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目