题目内容
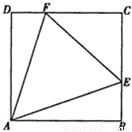
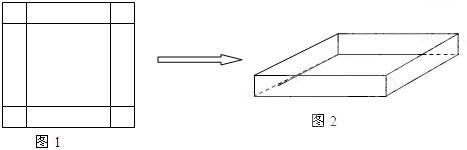
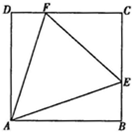
有一块边长为4米的正方形钢板,现对其进行切割,焊接成一个长方体无盖容器(切、焊损耗忽略不计),有人用数学知识作了如下设计:在钢板的四个角处各切去一个小正方形,剩余部分围成长方体.
(Ⅰ)求这种切割、焊接而成的长方体的最大容积V1.
(Ⅱ)请问:能重新设计,使所得长方体的容器的容积V2>V1吗?若能、给出你的一种设计方案.
(Ⅰ)求这种切割、焊接而成的长方体的最大容积V1.
(Ⅱ)请问:能重新设计,使所得长方体的容器的容积V2>V1吗?若能、给出你的一种设计方案.
分析:(I)设出小正方形的边长为x,则长方体的长宽都为4-2x,体积等于长×宽×高,求出体积的导数,令其等于零得出最大容积.
(II)主要对题意理解清楚,说的是材料有所浪费,想到在两个角切去小正方形,去下的小正方形焊到对边上组成新的长方体体积比原来的大.
(II)主要对题意理解清楚,说的是材料有所浪费,想到在两个角切去小正方形,去下的小正方形焊到对边上组成新的长方体体积比原来的大.
解答:解:(I)设切去正方形边长为x,则焊接成的长方体的底面边长为4-2x,高为x,
∴V1=(4-2x)2•x=4(x3-4x2+4x)(0<x<2).
∴V1′=4(3x2-8x+4).
令V1′=0,得x1=
,x2=2(舍去).
而V1′=12(x-
)(x-2),
又当x<
时,V1′>0;当
<x<2时,V1′<0,
∴当x=
时,V1取最大值
.
(II)重新设计方案如下:
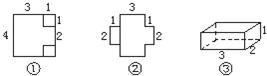
如图①,在正方形的两个角处各切下一个边长为1的小正方形;
如图②,将切下的小正方形焊在未切口的正方形一边的中间;
如图③,将图②焊成长方体容器.
新焊长方体容器底面是一长方形,长为3,宽为2,
此长方体容积V2=3×2×1=6,
显然V2>V1.
故第二种方案符合要求.
∴V1=(4-2x)2•x=4(x3-4x2+4x)(0<x<2).
∴V1′=4(3x2-8x+4).
令V1′=0,得x1=
| 2 |
| 3 |
而V1′=12(x-
| 2 |
| 3 |
又当x<
| 2 |
| 3 |
| 2 |
| 3 |
∴当x=
| 2 |
| 3 |
| 128 |
| 27 |
(II)重新设计方案如下:
如图①,在正方形的两个角处各切下一个边长为1的小正方形;
如图②,将切下的小正方形焊在未切口的正方形一边的中间;
如图③,将图②焊成长方体容器.
新焊长方体容器底面是一长方形,长为3,宽为2,
此长方体容积V2=3×2×1=6,
显然V2>V1.
故第二种方案符合要求.

点评:此题考查利用导数求闭区间的最值以及第二问是开放性问题,考查学生的实际操作能力.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案
相关题目
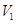 .
.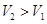 吗?若能、给出你的一种设计方案。
吗?若能、给出你的一种设计方案。