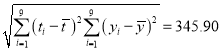题目内容
【题目】已知甲、乙两地生产同一种瓷器，现从两地的瓷器中随机抽取了一共300件统计质量指标值，得到如图的两个统计图，其中甲地瓷器的质量指标值在区间
和
的频数相等.
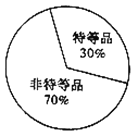
甲地瓷器质量频率分布直方图 乙地瓷器质量扇形统计图
（1）求直方图中
的值，并估计甲地瓷器质量指标值的平均值；（同一组中的数据用区间的中点值作代表）
（2）规定该种瓷器的质量指标值不低于125为特等品，且已知样本中甲地的特等品比乙地的特等品多10个，结合乙地瓷器质量扇形统计图完成下面的
列联表，并判断是否有95%的把握认为甲、乙两地的瓷器质量有差异？
物等品 | 非特等品 | 合计 | |
甲地 | |||
乙地 | |||
合计 |
附：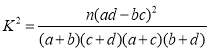
，其中
.
| 0.10 | 0.05 | 0.025 | 0.01 |
| 2.706 | 3.841 | 5.024 | 6.635 |
【答案】（1）
；（2）见解析
【解析】
(1)根据频率直方图和各组数据的频率和为1列出方程，可求得
，再运用各组数据中的区间的中点值乘以该组的频率之和可估计出甲地瓷器质量指标值的平均值；
(2)根据样本中甲地的特等品比乙地的特等品多10个，求得从甲地的瓷器中随机抽取的产品数和从乙地的瓷器中随机抽取的产品数，再根据甲地瓷器质量频率分布直方图和乙地瓷器质量扇形统计图完成的列联表，计算出
，对照表格中的数据可得结论.
(1)由频率直方图得：
，解得
，
估计甲地瓷器质量指标值的平均值为：
；
(2)设从甲地的瓷器中随机抽取了
件产品，则从乙地的瓷器中随机抽取了
件产品，
∵样本中甲地的特等品比乙地的特等品多10个，∴
，解得
，
∴根据甲地瓷器质量频率分布直方图和乙地瓷器质量扇形统计图完成的列联表如下表所示：
物等品 | 非特等品 | 合计 | |
甲地 | 40 | 160 | 200 |
乙地 | 30 | 70 | 100 |
合计 | 70 | 230 | 300 |
∴
，
∴没有95%的把握认为甲、乙两地的瓷器质量有差异.
练习册系列答案
相关题目
