题目内容
已知数列{an}前n项和Sn=n2+n
(1)求数列{an}的通项公式;
(2)令bn=
,求证:数列{bn}的前n项和Tn<
.
(1)求数列{an}的通项公式;
(2)令bn=
| 1 |
| anan+1 |
| 1 |
| 4 |
考点:数列与不等式的综合,数列的求和
专题:等差数列与等比数列,不等式的解法及应用
分析:(1)运用an=Sn-Sn-1,(n>1)公式求解,注意n=1,(2)运用裂项法求解,放缩证明.
解答:
解:(1)∵数列{an}前n项和Sn=n2+n,
∴当n=1时,a1=2,
当n≥2时,an=n2+n-(n-1)2-(n-1)=2n
∴数列{an}的通项公式an=2n
(2)由(1)知当数列{an}的通项公式:an=2n,
∵an+1-an=2,
∴bn=
×(
-
),
∴Tn=
×[
-
+
-
+…+
-
]
=
×(
-
)=
×(
-
)=
-
<
,
∴Tn<
,
∴当n=1时,a1=2,
当n≥2时,an=n2+n-(n-1)2-(n-1)=2n
∴数列{an}的通项公式an=2n
(2)由(1)知当数列{an}的通项公式:an=2n,
∵an+1-an=2,
∴bn=
| 1 |
| 2 |
| 1 |
| an |
| 1 |
| an+1 |
∴Tn=
| 1 |
| 2 |
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| a2 |
| 1 |
| a3 |
| 1 |
| an |
| 1 |
| an+1 |
=
| 1 |
| 2 |
| 1 |
| a1 |
| 1 |
| an+1 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2n+2 |
| 1 |
| 4 |
| 1 |
| 4n+4 |
| 1 |
| 4 |
∴Tn<
| 1 |
| 4 |
点评:本题考查了运用前n项和公式求解通项,放缩法求解有关的数列的n项和,属于中档题.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
满足{a,b}∪B={a,b,c}的集合B的个数是( )
| A、1 | B、2 | C、3 | D、4 |
对一切实数x,当a<b时,二次函数f(x)=ax2+bx+c的值恒为非负数,则b-2a-
的最大值为( )
| c |
| 2 |
| A、0 | B、1 | C、2 | D、-1 |
若实数x,y满足不等式
,且目标函数z=x-2y的最大值为( )
|
| A、1 | B、2 | C、3 | D、4 |
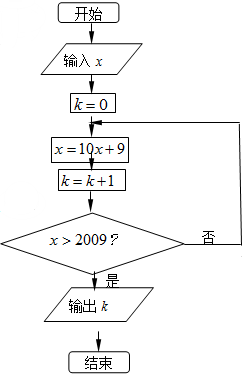 按如如图所示的程序框图运算.
按如如图所示的程序框图运算.