题目内容
【题目】如图,在三棱柱![]() 中,
中,![]() ,
,![]() ,且
,且![]() ,
,![]() 底面
底面![]() ,
,![]() 为
为![]() 中点,点
中点,点![]() 为
为![]() 上一点.
上一点.
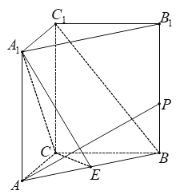
(1)求证: ![]()
![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值;
的余弦值;
(3)设![]() ,若
,若![]()
![]()
![]() ,写出
,写出![]() 的值(不需写过程).
的值(不需写过程).
【答案】(1)见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)证明![]()
![]() 平面
平面![]() ,只要在面
,只要在面![]() 内找到一条直线与
内找到一条直线与![]() 平行;
平行;
(2)以![]() ,
,![]() ,
,![]() 分别为x,y,z轴建立空间直角坐标系,写出两个面的法向量,再求法向量的夹角,结合图形发现二面角的平面角为钝角,从而求得二面角的余弦值。
分别为x,y,z轴建立空间直角坐标系,写出两个面的法向量,再求法向量的夹角,结合图形发现二面角的平面角为钝角,从而求得二面角的余弦值。
(3)由![]()
![]()
![]() ,
,![]()
![]()
![]() 可证得
可证得![]()
![]() 平面
平面![]() ,进而得到
,进而得到![]()
![]()
![]() ,再利用相似得到
,再利用相似得到![]() 为
为![]() 中点。
中点。
(1)连接![]() 交
交![]() 于
于![]() ,连接
,连接![]() ,
,
因为四边形![]() 为矩形,
为矩形,![]() ,
,![]() 为对角线,
为对角线,
所以![]() 为
为![]() 中点,又因为
中点,又因为![]() 为
为![]() 中点,
中点,
所以![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() //平面
//平面![]() .
.
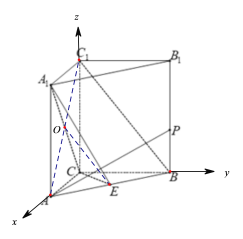
(2)因为![]() 底面
底面![]() ,所以
,所以![]() 底面
底面![]() ,
,
又![]() ,所以以
,所以以![]() ,
,![]() ,
,![]() 分别为x,y,z轴建立空间直角坐标系.
分别为x,y,z轴建立空间直角坐标系.
则![]() ,
,![]() ,
,![]() ,
,![]() .
.![]() ,
,![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,则有
,则有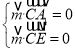 ,即
,即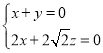
令![]() ,则
,则![]() .
.
由题意![]() 底面
底面![]() ,所以
,所以![]() 为平面
为平面![]() 的法向量,
的法向量,
所以![]() ,又由图可知二面角
,又由图可知二面角![]() 为钝二面角,
为钝二面角,
所以二面角![]() 的余弦值为
的余弦值为![]() 。
。
(3)![]() .
.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
【题目】某企业2018年招聘员工,其中![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 五种岗位的应聘人数、录用人数和录用比例(精确到1%)如下:
五种岗位的应聘人数、录用人数和录用比例(精确到1%)如下:
岗位 | 男性 应聘人数 | 男性 录用人数 | 男性 录用比例 | 女性 应聘人数 | 女性 录用人数 | 女性 录用比例 |
| 269 | 167 |
| 40 | 24 |
|
| 40 | 12 |
| 202 | 62 |
|
| 177 | 57 |
| 184 | 59 |
|
| 44 | 26 |
| 38 | 22 |
|
| 3 | 2 |
| 3 | 2 |
|
总计 | 533 | 264 |
| 467 | 169 |
|
(1)从表中所有应聘人员中随机选择1人,试估计此人被录用的概率;
(2)从应聘![]() 岗位的6人中随机选择2人.记
岗位的6人中随机选择2人.记![]() 为这2人中被录用的人数,求
为这2人中被录用的人数,求![]() 的分布列和数学期望;
的分布列和数学期望;
(3)表中![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 各岗位的男性、女性录用比例都接近(二者之差的绝对值不大于
各岗位的男性、女性录用比例都接近(二者之差的绝对值不大于![]() ),但男性的总录用比例却明显高于女性的总录用比例.研究发现,若只考虑其中某四种岗位,则男性、女性的总录用比例也接近,请写出这四种岗位.(只需写出结论)
),但男性的总录用比例却明显高于女性的总录用比例.研究发现,若只考虑其中某四种岗位,则男性、女性的总录用比例也接近,请写出这四种岗位.(只需写出结论)

