题目内容
已知如图1,在梯形ABCD中,AD∥BC,∠ABC=| π | 2 |
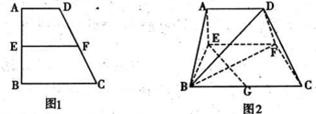
(1)当AE为何值时,有BD丄EG?
(2)设AE=x,以F、B、C、D为顶点的三梭锥的体积记为f(x),求f(x)的最大值;并求此时二面角D-BF-C的余弦值.
分析:(1)以点E为坐标原点,射线EB为X轴正半轴,建立如图所示的直角坐标系E-XYZ,设AE=x,得出各点的坐标,表示出BD与EG对应的向量,令它们的内积为0建立方程,求出x的值,得出两直线垂直的条件;
(2)先由体积公式计算出f(x),,利用基本不等式求出函数的最大值据等号成立的条件得到AE的值,由此得到有关各点的坐标,设出法向量,求出两个半平面的法向量由公式求出夹角的余弦即可
(2)先由体积公式计算出f(x),,利用基本不等式求出函数的最大值据等号成立的条件得到AE的值,由此得到有关各点的坐标,设出法向量,求出两个半平面的法向量由公式求出夹角的余弦即可
解答: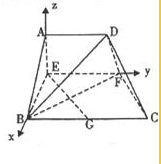 解:(1)以点E为坐标原点,射线EB为X轴正半轴,建立如图所示的直角坐标系E-XYZ,设AE=x,则E(0,0,0),B(2-x,0,0),D(0,1,x),G(2-x,1,0),
解:(1)以点E为坐标原点,射线EB为X轴正半轴,建立如图所示的直角坐标系E-XYZ,设AE=x,则E(0,0,0),B(2-x,0,0),D(0,1,x),G(2-x,1,0),
∴
=(x-2,1,x),
=(2-x,1,0),
∵BD丄EG,
∴
•
=0,即(x-2)(2-x)+1=0,解得x=1或x=3,
又在图1中AB=2,
∴x=1,故AE=1时有BD丄EG;
(2)∵AD∥面BEC,
∴f(x)=VD-BCF=VA-BCF=
×S△BCF×AE=
×
× 2(2-x)x≤
×(
)2=
.
设平面DBF的法向量为
=(x,y,z),
∵AE=1,B(1,0,0),D(0,1,1),F(0,
,0),
∴
=(-1,
,0),
=(-1,1,1),则
,即
,令y=2,得
=(3,2,1),
∵AE⊥面BCF,
∴面BCF的一个法向量为
=(0,0,1),则cos<
,
>=
=
,
由于所求的二面角D-BF-C的平面角是钝角,所以此二面角的余弦值为-
 解:(1)以点E为坐标原点,射线EB为X轴正半轴,建立如图所示的直角坐标系E-XYZ,设AE=x,则E(0,0,0),B(2-x,0,0),D(0,1,x),G(2-x,1,0),
解:(1)以点E为坐标原点,射线EB为X轴正半轴,建立如图所示的直角坐标系E-XYZ,设AE=x,则E(0,0,0),B(2-x,0,0),D(0,1,x),G(2-x,1,0),∴
| BD |
| EG |
∵BD丄EG,
∴
| BD |
| EG |
又在图1中AB=2,
∴x=1,故AE=1时有BD丄EG;
(2)∵AD∥面BEC,
∴f(x)=VD-BCF=VA-BCF=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 2-x+x |
| 2 |
| 1 |
| 3 |
设平面DBF的法向量为
| n1 |
∵AE=1,B(1,0,0),D(0,1,1),F(0,
| 3 |
| 2 |
∴
| BF |
| 3 |
| 2 |
| BD |
|
|
| n1 |
∵AE⊥面BCF,
∴面BCF的一个法向量为
| n2 |
| n1 |
| n2 |
| ||||
|
|
| ||
| 14 |
由于所求的二面角D-BF-C的平面角是钝角,所以此二面角的余弦值为-
| ||
| 14 |
点评:本题考查二面角的平面角及求法,解题的关键是建立空间坐标系,利用向量法求证线面垂直,线面平行,以及求面面夹角,利用空间向量求解立体几何中的线面,面面位置关系及求线面角,二面角,是空间向量的重要应用,引入空间向量,大大降低了求解立体几何问题时的问题时的推理难度,使得思考变得容易,但此法也有不足,从解题过程可以看出,用空间向量法解立体几何问题,运算量不少,计算时要严谨,莫因运算出错导致解题失败.本题要注意所求的二面角是钝角这一情况,据此判断出正确答案

练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目

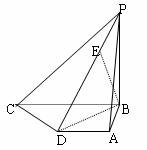 (II)求证:BE⊥平面PCD;
(II)求证:BE⊥平面PCD; (II)求证:BE⊥平面PCD;
(II)求证:BE⊥平面PCD;