题目内容
【题目】已知A(0,1)、B(0,2)、C(4t,2t2﹣1)(t∈R),⊙M是以AC为直径的圆,再以M为圆心、BM为半径作圆交x轴交于D、E两点.
(Ⅰ)若△CDE的面积为14,求此时⊙M的方程;
(Ⅱ)试问:是否存在一条平行于x轴的定直线与⊙M相切?若存在,求出此直线的方程;若不存在,请说明理由;
(Ⅲ)求 ![]() 的最大值,并求此时∠DBE的大小.
的最大值,并求此时∠DBE的大小.
【答案】解:(Ⅰ)由题意得,B(0,2)、M(2t,t2),
∴|BM|= ![]() =
= ![]() ;
;
∴以M为圆心、BM为半径的圆方程为(x﹣2t)2+(y﹣t2)2=t4+4,
∴其交x轴的弦 ![]() ,
,
∴ ![]() ,解得,t=±2,
,解得,t=±2,
∴⊙M的方程为(x±4)2+(y﹣4)2=20;
(Ⅱ)假设存在存在一条平行于x轴的定直线与⊙M相切;
∵ ![]() ,yM=t2 ,
,yM=t2 ,
∴存在一条平行于x轴的定直线y=﹣1与⊙M相切;
(Ⅲ)在△BDE中,设∠DBE=θ,且DE为弦,故 ![]() ,
,
由(Ⅰ)得,DE=4,在△BDE中,DE边上的高为2;
由三角形的面积相等得:![]() ,
,
∴ ![]() ;
;
由余弦定理得,DE2=BD2+BE2﹣2BDBE×cosθ,
∴ ![]() ,
,
∴ ![]() ,
,
∴ ![]() =
= 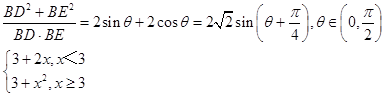 ,
,
故当 ![]() 时,
时, ![]() 的最大值为
的最大值为 ![]()
【解析】(Ⅰ)由题意求出圆心M的坐标、半径BM的长度,用t圆方程求交x轴的弦长,再由△CDE的面积为14求出t.(Ⅱ)先假设存在一条平行于x轴的定直线与⊙M相切,再利用圆心M到直线的距离等于半径M,求解.(Ⅲ)对式子 ![]() 通分后观察特点,在△BDE中,设∠DEB=θ,用三角形的面积相等和余弦定理用θ表示所求的式子,再进行整理后由正弦函数的单调性求最大值及θ.
通分后观察特点,在△BDE中,设∠DEB=θ,用三角形的面积相等和余弦定理用θ表示所求的式子,再进行整理后由正弦函数的单调性求最大值及θ.
【考点精析】利用圆的标准方程对题目进行判断即可得到答案,需要熟知圆的标准方程:![]() ;圆心为A(a,b),半径为r的圆的方程.
;圆心为A(a,b),半径为r的圆的方程.

练习册系列答案
相关题目