题目内容
设函数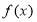 的定义域为
的定义域为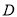 ,若
,若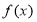 满足条件:存在
满足条件:存在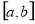
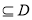 ,使
,使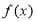 在
在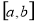 上的值域是
上的值域是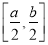 ,则成为“倍缩函数”,若函数
,则成为“倍缩函数”,若函数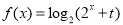 为“倍缩函数”,则
为“倍缩函数”,则 的范围是( )
的范围是( )
A.(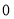 ,
,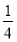 ) B.(
) B.(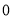 ,
,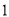 )
)
C.( ,
,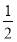 ) D.(
) D.(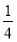 ,
,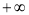 )
)
练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
题目内容
设函数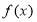 的定义域为
的定义域为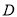 ,若
,若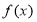 满足条件:存在
满足条件:存在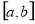
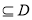 ,使
,使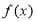 在
在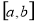 上的值域是
上的值域是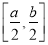 ,则成为“倍缩函数”,若函数
,则成为“倍缩函数”,若函数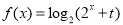 为“倍缩函数”,则
为“倍缩函数”,则 的范围是( )
的范围是( )
A.(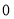 ,
,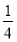 ) B.(
) B.(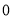 ,
,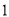 )
)
C.( ,
,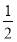 ) D.(
) D.(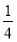 ,
,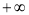 )
)
 科学实验活动册系列答案
科学实验活动册系列答案