题目内容
【题目】已知函数f(x)=loga(x+a)(a>0且a≠1)的图象过点(﹣1,0),g(x)=f(x)+f(﹣x).
(Ⅰ)求函数g(x)的定义域;
(Ⅱ)写出函数g(x)的单调区间,并求g(x)的最大值.
【答案】(Ⅰ)(﹣2,2),(Ⅱ)单调增区间(﹣2,0),单调递减区间(0,2),最大值2
【解析】
(Ⅰ)根据函数过点(﹣1,0),计算得到a=2,代入得到g(x)=f(x)+f(﹣x)
![]() ,定义域满足
,定义域满足![]() 得到答案.
得到答案.
(Ⅱ)利用复合函数的单调性到单调增区间(﹣2,0),单调递减区间(0,2),再计算最值得到答案.
(Ⅰ)f(x)=loga(x+a)(a>0且a≠1)的图象过点(﹣1,0),∴a﹣1=1即a=2,
∴g(x)=f(x)+f(﹣x)=log2(x+2)+log2(﹣x+2)![]()
由题意可得,![]() ,即﹣2<x<2
,即﹣2<x<2
∴函数g(x)的定义域(﹣2,2)
(Ⅱ)![]()
根据复合函数的单调性可知g(x)的单调增区间(﹣2,0),单调递减区间(0,2)
当x=0时,g(x)取得最大值2.

 名校课堂系列答案
名校课堂系列答案【题目】随着西部大开发的深入,西南地区的大学越来越受到广大考生的青睐,下表是西南地区某大学近五年的录取平均分与省一本线对比表:
年份 | 2014 | 2015 | 2016 | 2017 | 2018 |
年份代码 | 1 | 2 | 3 | 4 | 5 |
省一本线 | 505 | 500 | 525 | 500 | 530 |
录取平均分533 | 534 | 566 | 547 | 580 | |
录取平均分与省一本线分差y | 28 | 34 | 41 | 47 | 50 |
(1)根据上表数据可知,y与t之间存在线性相关关系,求y关于t的线性回归方程;
(2)据以往数据可知,该大学每年的录取分数X服从正态分布![]() ,其中
,其中![]() 为当年该大学的录取平均分,假设2019年该省一本线为520分,李华2019年高考考了569分,他很喜欢这所大学,想第一志愿填报,请利用概率与统计知识,给李华一个合理的建议.(第一志愿录取可能性低于
为当年该大学的录取平均分,假设2019年该省一本线为520分,李华2019年高考考了569分,他很喜欢这所大学,想第一志愿填报,请利用概率与统计知识,给李华一个合理的建议.(第一志愿录取可能性低于![]() ,则建议谨慎报考)
,则建议谨慎报考)
参考公式: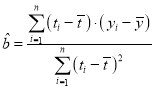 ,
,![]() .
.
参考数据:![]() ,
,![]() .
.




