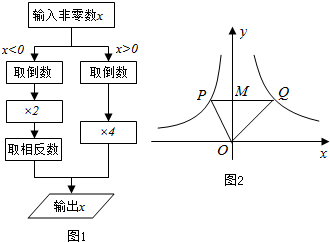
题目内容
4.连续抛掷同一颗均匀的骰子,令第i次得到的点数为ai,若存在正整数k,使a1+a2+…+ak=6,则称k为你的幸运数字.(1)求你的幸运数字为3的概率;
(2)若k=1,则你的得分为6分;若k=2,则你的得分为4分;若k=3,则你的得分为2分;若抛掷三次还没找到你的幸运数字则记0分,求得分ξ的分布列和数学期望.
分析 (1)设“连续抛掷k次骰子,和为6”为事件A,则它包含事件A1、A2,A3,其中A1:三次恰好均为2;A2:三次中恰好1,2,3各一次.A3:三次中有两次均为1,一次为4,A1,A2为互斥事件,由此能求出k=3的概率.
(2)由已知得ξ的可能取值为6,4,2,0,分别求出相应的概率,由此能求出ξ的分布列和Eξ.
解答 解:(1)设“连续抛掷k次骰子,和为6”为事件A,则它包含事件A1、A2,A3,
其中A1:三次恰好均为2;A2:三次中恰好1,2,3各一次.A3:三次中有两次均为1,一次为4,
A1,A2为互斥事件,则k=3的概率:
P(A)=P(A1)+P(A2)+P(A3)
=${C}_{3}^{3}(\frac{1}{6})^{3}$+${C}_{3}^{1}•\frac{1}{6}•{C}_{2}^{1}•\frac{1}{6}•{C}_{1}^{1}•\frac{1}{6}$+${C}_{3}^{2}(\frac{1}{6})^{2}$$•\frac{1}{6}$=$\frac{5}{108}$.
(2)由已知得ξ的可能取值为6,4,2,0,
P(ξ=6)=$\frac{1}{6}$,
P(ξ=4)=$(\frac{1}{6})^{2}$+${C}_{2}^{1}•\frac{1}{6}•\frac{1}{6}$+${C}_{2}^{1}•\frac{1}{6}•\frac{1}{6}$=$\frac{5}{36}$,
P(ξ=2)=${C}_{3}^{3}(\frac{1}{6})^{3}$+${C}_{3}^{1}•\frac{1}{6}•{C}_{2}^{1}•\frac{1}{6}•{C}_{1}^{1}•\frac{1}{6}$+${C}_{3}^{2}(\frac{1}{6})^{2}$$•\frac{1}{6}$=$\frac{5}{108}$.
P(ξ=0)=1-$\frac{1}{6}$-$\frac{5}{36}$-$\frac{5}{108}$=$\frac{35}{54}$,
∴ξ的分布列为:
| ξ | 6 | 4 | 2 | 0 |
| P | $\frac{1}{6}$ | $\frac{5}{36}$ | $\frac{5}{108}$ | $\frac{35}{54}$ |
点评 本题考查概率的求法,考查离散型随机变量的分布列和数学期望的求法,是中档题,解题时要认真审题,注意互斥事件概率加法公式的合理运用.

| A. | $\frac{5}{3}$ | B. | $\frac{3}{5}$ | C. | ±$\frac{3}{5}$ | D. | ±$\frac{5}{3}$ |
 满足:①
满足:① ;②
;②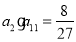 ;③
;③ .
. ,问:是否存在常数
,问:是否存在常数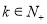 ,使得
,使得 对于任意
对于任意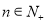 恒成立?若存在,请求出
恒成立?若存在,请求出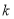 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.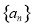 的前
的前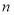 项和
项和 ,则
,则 ____________.
____________.