题目内容
设直线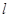 :
: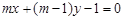 ,圆
,圆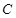 :
: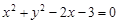 ,则( )
,则( )
A.对任意实数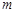 ,直线
,直线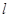 恒过定点
恒过定点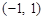
B.存在实数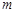 ,使直线
,使直线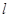 与圆
与圆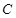 无公共点
无公共点
C.若圆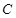 上存在两点关于直线
上存在两点关于直线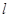 对称,则
对称,则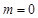
D.若直线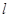 与圆
与圆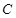 相交于
相交于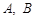 两点,则
两点,则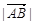 的最小值是
的最小值是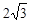
【答案】
D
【解析】
试题分析:由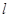 :
: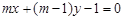 得:
得: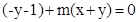 ,所以过定点
,所以过定点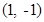 ,选项A错。又定点
,选项A错。又定点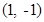 与圆心的距离为1小于半径2,所以定点在圆内,所以选项B错。若圆
与圆心的距离为1小于半径2,所以定点在圆内,所以选项B错。若圆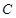 上存在两点关于直线
上存在两点关于直线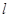 对称,则直线过圆心,求得m=1,所以选项C错。当定点为AB中点时,线段AB最短,求得
对称,则直线过圆心,求得m=1,所以选项C错。当定点为AB中点时,线段AB最短,求得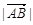 的最小值是
的最小值是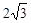 ,所以选项D对。
,所以选项D对。
考点:本题考查直线系方程、圆的一般式方程以及直线与圆的位置关系。
点评:直线系过定点的求法要当心,一般转化为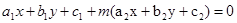 这种形式,联立
这种形式,联立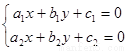 求解即为定点。
求解即为定点。

练习册系列答案
相关题目
 (2012•荆州模拟)请在下面两题中选做一题,如果多做,则按所做的第一题计分.
(2012•荆州模拟)请在下面两题中选做一题,如果多做,则按所做的第一题计分. 和
和 为椭圆的两个焦点,以
为椭圆的两个焦点,以 为圆心作圆,已知圆
为圆心作圆,已知圆 点,若直线
点,若直线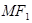 恰与圆
恰与圆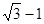 B.
B. 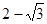 C.
C.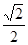 D.
D. 
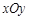 中,设直线
中,设直线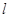 :
: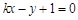 与圆
与圆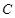 :
: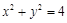 相交于
相交于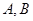 两点,以
两点,以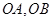 为邻边作平行四边形
为邻边作平行四边形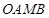 ,若点
,若点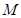 在圆
在圆 。
。