题目内容
12分)某城市有一块不规则的绿地如图所示,城建部门欲在该地上建造一个底座为三角形的环境标志,小李、小王设计的底座形状分别为△ABC、△ABD,经测量AD=BD=14,BC=10,AC=16,∠C=∠D.
(I)求AB的长度;
(Ⅱ)若建造环境标志的费用与用地面积成正比,不考虑其他因素,小李、小王谁的设计使建造费用最低,请说明理由.
(Ⅰ)A、B两点的距离为14.(Ⅱ)
解析试题分析:(Ⅰ)在△ABC中,由余弦定理得cosC 的值,在△ABD中,由余弦定理得cosD 的值,由∠C=∠D得 cosC=cosD,求得AB=7,从而得出结论.
(Ⅱ)小李的设计符合要求,因为由条件可得 S△ABD>S△ABC,再由AD=BD=AB=7,得△ABD是等边三角形.由此求得S△ABC的值,再乘以5000,即得所求.
解:(Ⅰ)在 中,由余弦定理得
中,由余弦定理得 ①
①
在 中,由余弦定理及
中,由余弦定理及 整理得
整理得 ②………4分
②………4分
由①②得:
整理可得  ,……………6分
,……………6分
又 为三角形的内角,所以
为三角形的内角,所以 ,
,
又 ,
, ,所以
,所以 是等边三角形,
是等边三角形,
故 ,即A、B两点的距离为14.……………8分
,即A、B两点的距离为14.……………8分
(Ⅱ)小李的设计符合要求.理由如下:

因为
 …………12分
…………12分
所以
考点:本试题主要考查了余弦定理的应用,考查三角形面积的计算,考查利用数学知识解决实际问题的能力,属于中档题
点评:解决该试题的关键是能灵活运用余弦定理得到cosD的值。

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
 ,∠ADE=
,∠ADE= 。
。

 。
。 的值;
的值; ,求
,求 和
和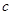 。
。 中,
中, 的对边分别为
的对边分别为 且
且 成等差数列.(1)求
成等差数列.(1)求 的值;(2)求
的值;(2)求 的取值范围。
的取值范围。 中,内角
中,内角 对边的边长分别是
对边的边长分别是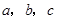 ,已知
,已知 ,
, ,
, ,求
,求 中,角A、B、C所对的边分别是
中,角A、B、C所对的边分别是  ,且
,且 ="2,"
="2,"  .
. 的值.
的值. =3,求b,c的值.
=3,求b,c的值.  中,角
中,角 的对边分别为
的对边分别为 ,已知
,已知 ,且
,且 ,
, ,
, (2)△
(2)△ 中,
中, .
. 的值; (2)若
的值; (2)若 ,
, ,求
,求 和
和 的值。
的值。 中,角
中,角 的对边分别为
的对边分别为 ,
, ,
,
 的值;(Ⅱ)若
的值;(Ⅱ)若 ,求
,求 的值.
的值.