题目内容
已知函数
（Ⅰ）若函数y=f(x)的图象切x轴于点（2，0），求a、b的值；
（Ⅱ）设函数y=f(x) 
的图象上任意一点的切线斜率为k，试求
的充要条件；
（Ⅲ）若函数y=f(x)的图象上任意不同的两点的连线的斜率小于1，求证
。
（Ⅰ）
， 
（Ⅱ）
（Ⅲ）证明见解析
解析:
（Ⅰ）
…………………………………………1分
由
得， ………………………………………………2分
又
得 ……………………………………………………3分
（Ⅱ）k＝
，
对任意的
，即
对任意的恒成立……4分
等价于
对任意的恒成立。…………………………5分
令g(x)＝
，h(x)＝
，
则
， …………………………………………6分
，当且仅当
时“＝”成立，
…………7分
h(x)＝在（0，1）上为增函数，h(x)max＜2……………………………8分
……………………………………………………………………9分
（Ⅲ）设
则
＝
……10分
即
，对
恒成立…………………………11分
，对
恒成立
即
对恒成立…………………………13分
解得
……………………………………………………14分
练习册系列答案
智趣暑假温故知新系列答案
英语小英雄天天默写系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
，
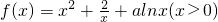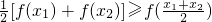成立，则称函数y=f（x）为区间D上的“凹函 数”．试证当a≤0时，f（x）为“凹函数”．
，
成立，则称函数y=f（x）为区间D上的“凹函 数”．试证当a≤0时，f（x）为“凹函数”．
，
成立，则称函数y=f（x）为区间D上的“凹函 数”．试证当a≤0时，f（x）为“凹函数”．