题目内容
已知函数 ,
,(Ⅰ) 若f(x)在[1,+∞)上单调递增,求a的取值范围;
(Ⅱ)若定义在区间D上的函数y=f(x)对于区间D上的任意两个值x1、x2总有以下不等式
 成立,则称函数y=f(x)为区间D上的“凹函 数”.试证当a≤0时,f(x)为“凹函数”.
成立,则称函数y=f(x)为区间D上的“凹函 数”.试证当a≤0时,f(x)为“凹函数”.
【答案】分析:(Ⅰ)由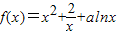 ,得
,得 ,由函数为[1,+∞)上单调增函数,知f′(x)≥0在[1,+∞)上恒成立,即不等式
,由函数为[1,+∞)上单调增函数,知f′(x)≥0在[1,+∞)上恒成立,即不等式 在[1,+∞)上恒成立.由此能求出a的取值范围.
在[1,+∞)上恒成立.由此能求出a的取值范围.
(Ⅱ)由 ,得
,得 =
= ,
, ,由此入手能够证明当a≤0时,f(x)为“凹函数”.
,由此入手能够证明当a≤0时,f(x)为“凹函数”.
解答:解:(Ⅰ)由 ,
,
得 …(2分)
…(2分)
函数为[1,+∞)上单调函数.
若函数为[1,+∞)上单调增函数,
则f′(x)≥0在[1,+∞)上恒成立,
即不等式 在[1,+∞)上恒成立.
在[1,+∞)上恒成立.
也即 在[1,+∞)上恒成立.…(3分)
在[1,+∞)上恒成立.…(3分)
令 ,上述问题等价于a≥φ(x)max,
,上述问题等价于a≥φ(x)max,
而 为在[1,+∞)上的减函数,
为在[1,+∞)上的减函数,
则φ(x)max=φ(1)=0,于是a≥0为所求.…(5分)
(Ⅱ)证明:由
得
=
 …(7分)
…(7分)
而 ①…(9分)
①…(9分)
又(x1+x2)2=(x12+x22)+2x1x2≥4x1x2,
∴ ②…(10分)
②…(10分)
∵ ,
,
∴ ,
,
∵a≤0
∴ ③…(12分)
③…(12分)
由①、②、③得
即 ,从而由凹函数的定义可知函数为凹函数.…(13分)
,从而由凹函数的定义可知函数为凹函数.…(13分)
点评:本题考查函数的恒等性在生产实际中的应用,考查运算求解能力,推理论证能力;考查函数与方程思想,化归与转化思想.综合性强,是高考的重点,易错点是知识体系不牢固.
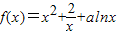 ,得
,得 ,由函数为[1,+∞)上单调增函数,知f′(x)≥0在[1,+∞)上恒成立,即不等式
,由函数为[1,+∞)上单调增函数,知f′(x)≥0在[1,+∞)上恒成立,即不等式 在[1,+∞)上恒成立.由此能求出a的取值范围.
在[1,+∞)上恒成立.由此能求出a的取值范围.(Ⅱ)由
 ,得
,得 =
= ,
, ,由此入手能够证明当a≤0时,f(x)为“凹函数”.
,由此入手能够证明当a≤0时,f(x)为“凹函数”.解答:解:(Ⅰ)由
 ,
,得
 …(2分)
…(2分)函数为[1,+∞)上单调函数.
若函数为[1,+∞)上单调增函数,
则f′(x)≥0在[1,+∞)上恒成立,
即不等式
 在[1,+∞)上恒成立.
在[1,+∞)上恒成立.也即
 在[1,+∞)上恒成立.…(3分)
在[1,+∞)上恒成立.…(3分)令
 ,上述问题等价于a≥φ(x)max,
,上述问题等价于a≥φ(x)max,而
 为在[1,+∞)上的减函数,
为在[1,+∞)上的减函数,则φ(x)max=φ(1)=0,于是a≥0为所求.…(5分)
(Ⅱ)证明:由

得

=

 …(7分)
…(7分)而
 ①…(9分)
①…(9分)又(x1+x2)2=(x12+x22)+2x1x2≥4x1x2,
∴
 ②…(10分)
②…(10分)∵
 ,
,∴
 ,
,∵a≤0
∴
 ③…(12分)
③…(12分)由①、②、③得

即
 ,从而由凹函数的定义可知函数为凹函数.…(13分)
,从而由凹函数的定义可知函数为凹函数.…(13分)点评:本题考查函数的恒等性在生产实际中的应用,考查运算求解能力,推理论证能力;考查函数与方程思想,化归与转化思想.综合性强,是高考的重点,易错点是知识体系不牢固.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
 ,
,
 与曲线
与曲线 在它们的交点(1,c)处具有公共切线,求
在它们的交点(1,c)处具有公共切线,求 ,
,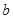 的值;
的值; ,
, 时,若函数
时,若函数 在区间[
在区间[ ,2]上的最大值为28,求
,2]上的最大值为28,求 ,
, 在
在 上的最大值为
上的最大值为 ,求实数
,求实数 的值;
的值; ,都有
,都有 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围; ,对任意给定的正实数
,对任意给定的正实数 上是否存在两点
上是否存在两点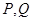 ,使得
,使得 是以
是以 (
( 轴上?请说明理由。
轴上?请说明理由。