题目内容
以下叙述正确的是( )
分析:根据倾斜角为90°的直线斜率不存在,可判断A,根据平面上到两个定点的距离之和为同一个常数等于两定点距离时,动点的轨迹是线段,可判断B;根据圆心到直线的距离与半径的关系,可判断C;根据定比分点公式及圆的参数方程可判断D
解答:解:倾斜角为90°的直线斜率不存在,故平面直角坐标系下的每条直线一定有倾斜角与法向量,但是不一定都有斜率,即A说法正确
平面上到两个定点的距离之和为同一个常数等于两定点距离时,动点的轨迹是线段,即B说法不正确;
圆心C(3,0)到直线l:x+y-1=0的距离d=
,圆的半径r=4,故圆C上有四个点到直线l的距离为2,即C说法不正确
由P是圆C:(x-4)2+y2=4上的任意一点,故P点坐标为(4+2cosθ,2sinθ),由动点M分
(O为坐标原点)的比为λ(λ>0),可得M点的坐标为(
,
)(λ>0),则M的轨迹仍为一个圆,故D说法不正确
平面上到两个定点的距离之和为同一个常数等于两定点距离时,动点的轨迹是线段,即B说法不正确;
圆心C(3,0)到直线l:x+y-1=0的距离d=
| 2 |
由P是圆C:(x-4)2+y2=4上的任意一点,故P点坐标为(4+2cosθ,2sinθ),由动点M分
| OP |
| 4λ+2λcosθ |
| 1+λ |
| 2λsinθ |
| 1+λ |
点评:本题以命题的真假判断为载体考查了斜率的定义,椭圆的定义,直线与圆的位置关系,轨迹方程是解析几何比较综合的应用,难度较大.

练习册系列答案
相关题目
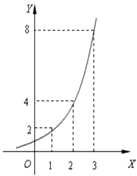 如图所示的是某池塘中的浮萍蔓延的面积(m2)与时间x(月)的关系:y=ax,有以下叙述:
如图所示的是某池塘中的浮萍蔓延的面积(m2)与时间x(月)的关系:y=ax,有以下叙述:①这个指数函数的底数是2;
②第5个月的浮萍的面积就会超过30m2;
③浮萍从4m2蔓延到12m2需要经过1.5个月;
④浮萍每个月增加的面积都相等;
⑤若浮萍蔓延到2m2、3m2、6m2所经过的时间分别为x1,x2,x3,则x1+x2=x3.
其中正确的是( )
| A、①② | B、①②⑤ | C、①②③④ | D、②③④⑤ |
一位母亲记录了她儿子3到9岁的身高,数据如下表:
|
(教材1.1例1变式)一位母亲记录了她儿子3岁到9岁的身高,数据如下:
| 年龄(岁) | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 身高(cm) | 94.8 | 104.2 | 108.7 | 117.8 | 124.3 | 130.8 | 139.0 |
由此建立了身高与年龄的回归模型:
y=73.93+7.19x,她用这个模型预测儿子10岁时的身高,则下列叙述正确的是( )
A.她儿子10岁时的身高一定145.83cm
B.她儿子10岁时的身高在145.83cm 以上
C.她儿子10岁时的身高在145.83cm 左右
D.她儿子10岁时的身高在145.83cm 以下