题目内容
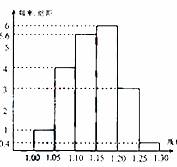
 为了了解一个小水库中养殖的鱼有关情况,从这个水库中多个不同位置捕捞出100条鱼,称得每条鱼的质量(单位:千克),并将所得数据分组,画出频率分布直方图(如图所示)
为了了解一个小水库中养殖的鱼有关情况,从这个水库中多个不同位置捕捞出100条鱼,称得每条鱼的质量(单位:千克),并将所得数据分组,画出频率分布直方图(如图所示)(Ⅰ)在表格中填写相应的频率;
| 分组 | 频率 |
| [1.00,1.05) | |
| [1.05,1.10) | |
| [1.10,1.15) | |
| [1.15,1.20) | |
| [1.20,1.25) | |
| [1.25,1.30] |
(Ⅲ)将上面捕捞的100条鱼分别作一记号后再放回水库,几天后再120条鱼,其中带有记号的鱼有6条,请根据这一情况来估计该水库中鱼的总条数.
【答案】分析:(1)根据频率分布直方图可知,矩形的高为 ,然后利用“频率=组距×
,然后利用“频率=组距× ”求出每组的频率,即可填全表格;
”求出每组的频率,即可填全表格;
(2)先求出数据落在[1.15,1.30)中的频率,然后利用样本数据落在[1.15,1.30)中的频率估计总体的概率;
(3)根据该水库中鱼的总条数= 进行求解即可.
进行求解即可.
解答:解:(Ⅰ)根据频率分布直方图可知,频率=组距× ,故可得下表
,故可得下表
(Ⅱ)0.30+0.15+0.02=0.47,所以数据落在[1.15,1.30)中的概率约为0.47.
(Ⅲ)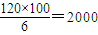 ,所以水库中鱼的总条数约为2000条.
,所以水库中鱼的总条数约为2000条.
点评:本题考查频率分布直方图,以及利用样本估计总体等有关知识,直方图中的各个矩形的面积代表了频率,所以各个矩形面积之和为1,同时考查了分析问题解决问题的能力,属于基础题.
 ,然后利用“频率=组距×
,然后利用“频率=组距× ”求出每组的频率,即可填全表格;
”求出每组的频率,即可填全表格;(2)先求出数据落在[1.15,1.30)中的频率,然后利用样本数据落在[1.15,1.30)中的频率估计总体的概率;
(3)根据该水库中鱼的总条数=
 进行求解即可.
进行求解即可.解答:解:(Ⅰ)根据频率分布直方图可知,频率=组距×
 ,故可得下表
,故可得下表| 分组 | 频率 |
| [1.00,1.05) | 0.05 |
| [1.05,1.10) | 0.20 |
| [1.10,1.15) | 0.28 |
| [1.15,1.20) | 0.30 |
| [1.20,1.25) | 0.15 |
| [1.25,1.30] | 0.02 |
(Ⅲ)
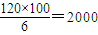 ,所以水库中鱼的总条数约为2000条.
,所以水库中鱼的总条数约为2000条.点评:本题考查频率分布直方图,以及利用样本估计总体等有关知识,直方图中的各个矩形的面积代表了频率,所以各个矩形面积之和为1,同时考查了分析问题解决问题的能力,属于基础题.

练习册系列答案
相关题目
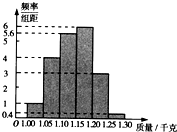 为了了解一个小水库中养殖的鱼有关情况,从这个水库中多个不同位置捕捞出100条鱼,称得每条鱼的质量(单位:千克),并将所得数据分组,画出频率分布直方图(如图所示)
为了了解一个小水库中养殖的鱼有关情况,从这个水库中多个不同位置捕捞出100条鱼,称得每条鱼的质量(单位:千克),并将所得数据分组,画出频率分布直方图(如图所示)(Ⅰ)在表格中填写相应的频率;
| 分组 | 频率 |
| [1.00,1.05) | |
| [1.05,1.10) | |
| [1.10,1.15) | |
| [1.15,1.20) | |
| [1.20,1.25) | |
| [1.25,1.30] |
(Ⅲ)将上面捕捞的100条鱼分别作一记号后再放回水库,几天后再120条鱼,其中带有记号的鱼有6条,请根据这一情况来估计该水库中鱼的总条数.
 为了了解一个小水库中养殖的鱼有关情况,从这个水库中多个不同位置捕捞出100条鱼,称得每条鱼的质量(单位:千克),并将所得数据分组,画出频率分布直方图(如图所示)
为了了解一个小水库中养殖的鱼有关情况,从这个水库中多个不同位置捕捞出100条鱼,称得每条鱼的质量(单位:千克),并将所得数据分组,画出频率分布直方图(如图所示)(Ⅰ)在表格中填写相应的频率;
| 分组 | 频率 |
| [1.00,1.05) | |
| [1.05,1.10) | |
| [1.10,1.15) | |
| [1.15,1.20) | |
| [1.20,1.25) | |
| [1.25,1.30] |
(Ⅲ)将上面捕捞的100条鱼分别作一记号后再放回水库,几天后再120条鱼,其中带有记号的鱼有6条,请根据这一情况来估计该水库中鱼的总条数.