Question

【题目】以圆x2+y2﹣2x﹣2y﹣1=0内横坐标与纵坐标均为整数的点为顶点的三角形的个数为（ ）
A.76
B.78
C.81
D.84

Answer 1

【答案】A
【解析】解：∵圆x2+y2﹣2x﹣2y﹣1=0化成标准形式，得 （x﹣1）2+（y﹣1）2=3
∴圆心C（1，1），半径r=
满足横坐标与纵坐标均为整数的点，且在圆内的点有
（0，0），（0，1），（0，2），（1，0），（1，1），（1，2），
（2，0），（2，1），（2，2）共9个点
9个点中任取3个，共有 =84种取法，其中三点共线的情况共有8种
∴这9个点能构成三角形的个数为84﹣8=76个
故选：A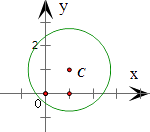

【考点精析】利用圆的一般方程对题目进行判断即可得到答案，需要熟知圆的一般方程的特点：(1)①x2和y2的系数相同，不等于0．②没有xy这样的二次项；(2)圆的一般方程中有三个特定的系数D、E、F，因之只要求出这三个系数，圆的方程就确定了；(3)、与圆的标准方程相比较，它是一种特殊的二元二次方程，代数特征明显，圆的标准方程则指出了圆心坐标与半径大小，几何特征较明显．