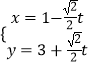题目内容
【题目】函数f(x)的定义域为D={x|x≠0},且满足对于任意x1 , x2∈D,有f(x1x2)=f(x1)+f(x2).
(1)求f(1)的值;
(2)判断f(x)的奇偶性并证明你的结论;
(3)如果f(4)=1,f(x﹣1)<2,且f(x)在(0,+∞)上是增函数,求x的取值范围.
【答案】
(1)解:∵对于任意x1,x2∈D,有f(x1x2)=f(x1)+f(x2),
∴令x1=x2=1,得f(1)=2f(1),∴f(1)=0.
(2)解:f(x)为偶函数.
证明:令x1=x2=﹣1,有f(1)=f(﹣1)+f(﹣1),∴f(﹣1)= ![]() f(1)=0.
f(1)=0.
令x1=﹣1,x2=x有f(﹣x)=f(﹣1)+f(x),∴f(﹣x)=f(x),∴f(x)为偶函数.
(3)解:依题设有f(4×4)=f(4)+f(4)=2,由(2)知,f(x)是偶函数,
∴f(x﹣1)<2f(|x﹣1|)<f(16).又f(x)在(0,+∞)上是增函数,
∴0<|x﹣1|<16,解之得﹣15<x<17且x≠1,∴x的取值范围是{x|﹣15<x<17且x≠1}.
【解析】(1)根据抽象函数的关系求得f(1)的值;(2)令x1=﹣1,x2=x,并结合抽象函数的关系及f(﹣1)的值判断函数的奇偶性;(3)根据f(4)=1及函数关系可求得函数值为2的自变量的值,再利用单调性变为自变量的不等式,从而求得x的取值范围.
【考点精析】关于本题考查的奇偶性与单调性的综合,需要了解奇函数在关于原点对称的区间上有相同的单调性;偶函数在关于原点对称的区间上有相反的单调性才能得出正确答案.

练习册系列答案
相关题目