题目内容
已知点A(7,-4),B(-5,6),求线段AB的垂直平分线的方程.
分析:设线段AB的中点为M(x0,y0),利用中点坐标公式可得M.设线段AB的垂直平分线的斜率k,则k•kAB=-1即可得出.
解答:解:设线段AB的中点为M(x0,y0),则
,∴M(1,1).
∵kAB=
=-
,∴线段AB的垂直平分线的斜率k=
.
∴线段AB的垂直平分线的方程为y-1=
(x-1),化为6x-5y-1=0.
|
∵kAB=
| -4-6 |
| 7-(-5) |
| 5 |
| 6 |
| 6 |
| 5 |
∴线段AB的垂直平分线的方程为y-1=
| 6 |
| 5 |
点评:本题考查了线段的垂直平分线的性质、中点坐标公式、相互垂直的直线斜率之间的关系,属于基础题.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
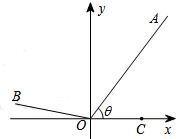 如图,已知点A(3,4),C(2,0),点O为坐标原点,点B在第二象限,且|OB|=3,记∠AOC=θ.高.
如图,已知点A(3,4),C(2,0),点O为坐标原点,点B在第二象限,且|OB|=3,记∠AOC=θ.高.