Question

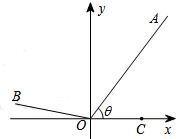如图，已知点A（3，4），C（2，0），点O为坐标原点，点B在第二象限，且|OB|=3，记∠AOC=θ．高．
（Ⅰ）求sin2θ的值；
（Ⅱ）若AB=7，求△BOC的面积．

Answer 1

分析：（Ⅰ）先由三角函数定义求sinθ、cosθ，再根据正弦的倍角公式求出sin2θ；
（Ⅱ）设点B坐标，然后列方程组解之，最后由三角形面积公式求得答案．

解答：解：（Ⅰ）∵A点的坐标为（3，4），∴OA=

32+42

=5，
∴sinθ=

4

5

，cosθ=

3

5

，
∴sin2θ=2sinθcosθ=

24

25

（Ⅱ）设B（x，y），由OB=3，AB=7得

x2+y2=9 (x-3)2+(x-4)2=49

解得y=-

9 3 +12

10

或y=

9 3 -12

10

，
又点B在第二象限，故y=

9 3 -12

10

．
∴△BOC的面积S=

1

2

OC•y=

9 3 -12

20

.

点评：本题考查三角函数定义、正弦的二倍角公式及方程思想．