Question

已知x，y满足约束条件

x-y≤0 x+y-1≥0 x-2y+2≥0

若的最小值为4，则z=x+3y+m，则m=（　　）

Answer 1

分析：作出可行域，求出交点的坐标，利用z=x+3y+m的最小值为4，可求m的值．

解答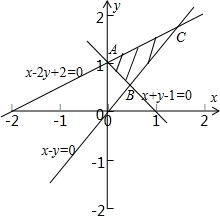：解：约束条件

x-y≤0 x+y-1≥0 x-2y+2≥0

的可行域，如图所示
由

x+y-1=0 x-2y+2=0

，可得B（

1

2

，

1

2

），
∵z=x+3y+m，
∴z在点B处取得最小值4，
∴

1

2

+

3

2

+m=4，
∴m=2．
故选B．

点评：在解决线性规划的小题时，我们常用“角点法”，其步骤为：①由约束条件画出可行域⇒②求出可行域各个角点的坐标⇒③将坐标逐一代入目标函数⇒④验证，求出最优解．