题目内容
设等比数列{an}的前n项和为Sn,已知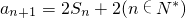 .
.
(1)求数列{an}的通项公式;
(2)在an与an+1之间插入n个数,使这n+2个数组成公差为dn的等差数列(如:在a1与a2之间插入1个数构成第一个等差数列,其公差为d1;在a2与a3之间插入2个数构成第二个等差数列,其公差为d2,…以此类推),设第n个等差数列的和是An.是否存在一个关于n的多项式g(n),使得An=g(n)dn对任意n∈N*恒成立?若存在,求出这个多项式;若不存在,请说明理由;
(3)对于(2)中的数列d1,d2,d3,…,dn,…,这个数列中是否存在不同的三项dm,dk,dp(其中正整数m,k,p成等差数列)成等比数列,若存在,求出这样的三项;若不存在,说明理由.
解:(1)n≥2时,由an+1=2Sn+2,得an=2Sn-1+
两式相减可得:an+1-an=2an,∴an+1=3an,即数列{an}的公比为3
∵n=1时,a2=2S1+2,∴3a1=2a1+2,解得a1=2,
∴an=2×3n-1;
(2)由(1)知an=2×3n-1,an+1=2×3n,
因为an+1=an+(n+1)dn,所以dn=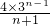
第n个等差数列的和是An=(n+2)an+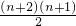 ×
×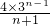 =4(n+2)×3n-1=(n+2)(n+1)dn,
=4(n+2)×3n-1=(n+2)(n+1)dn,
∴存在一个关于n的多项式g(n)=(n+2)(n+1),使得An=g(n)dn对任意n∈N*恒成立;
(3)假设在数列{dn}中存在dm,dk,dp(其中m,k,p成等差数列)成等比数列
则dk2=dmdp,即(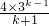 )2=
)2=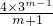 ×
×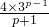
因为m,k,p成等差数列,所以m+p=2k①
上式可以化简为k2=mp②
由①②可得m=k=p这与题设矛盾
所以在数列{dn}中不存在三项dm,dk,dp(其中m,k,p成等差数列)成等比数列.
分析:(1)n≥2时,由an+1=2Sn+2,再写一式,两式相减,即可求得数列{an}的通项公式;
(2)先求得dn,从而可得第n个等差数列的和An,由此可得结论;
(3)利用反证法.假设在数列{dn}中存在dm,dk,dp(其中m,k,p成等差数列)成等比数列,由此可得m=k=p这与题设矛盾.
点评:本题考查数列通项公式的求解,考查等差数列的求和,考查反证法思想,确定数列的通项,利用数列的求和公式是关键.
两式相减可得:an+1-an=2an,∴an+1=3an,即数列{an}的公比为3
∵n=1时,a2=2S1+2,∴3a1=2a1+2,解得a1=2,
∴an=2×3n-1;
(2)由(1)知an=2×3n-1,an+1=2×3n,
因为an+1=an+(n+1)dn,所以dn=
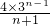
第n个等差数列的和是An=(n+2)an+
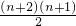 ×
×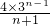 =4(n+2)×3n-1=(n+2)(n+1)dn,
=4(n+2)×3n-1=(n+2)(n+1)dn,∴存在一个关于n的多项式g(n)=(n+2)(n+1),使得An=g(n)dn对任意n∈N*恒成立;
(3)假设在数列{dn}中存在dm,dk,dp(其中m,k,p成等差数列)成等比数列
则dk2=dmdp,即(
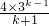 )2=
)2=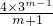 ×
×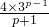
因为m,k,p成等差数列,所以m+p=2k①
上式可以化简为k2=mp②
由①②可得m=k=p这与题设矛盾
所以在数列{dn}中不存在三项dm,dk,dp(其中m,k,p成等差数列)成等比数列.
分析:(1)n≥2时,由an+1=2Sn+2,再写一式,两式相减,即可求得数列{an}的通项公式;
(2)先求得dn,从而可得第n个等差数列的和An,由此可得结论;
(3)利用反证法.假设在数列{dn}中存在dm,dk,dp(其中m,k,p成等差数列)成等比数列,由此可得m=k=p这与题设矛盾.
点评:本题考查数列通项公式的求解,考查等差数列的求和,考查反证法思想,确定数列的通项,利用数列的求和公式是关键.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案
相关题目
设等比数列{an}的前n项和为Sn,若8a2+a5=0,则下列式子中数值不能确定的是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
设等比数列{an}的前n项和为Sn,若
=3,则
=( )
| S6 |
| S3 |
| S9 |
| S6 |
A、
| ||
B、
| ||
C、
| ||
| D、1 |