题目内容
定义[x]表示不超过x的最大整数,记{x}=x-[x],其中对于0≤x≤316时,函数f(x)=sin2[x]+sin2{x}-1和函数g(x)=[x]•{x}-
-1的零点个数分别为m,n,则( )
| x |
| 3 |
分析:根据定义分别求出f(x)=0和g(x)=0,将函数方程转化为sin2[x]+sin2{x}-1=0和[x]•{x}=
+1,分别利用图象讨论两个函数零点的个数.
| x |
| 3 |
解答:解:由f(x)=sin2[x]+sin2{x}-1=0得sin2{x}=1-sin2[x]=cos2[x].
则{x}=
+2kπ+[x]或{x}=-
+2kπ+[x],
即{x}-[x]=
+2kπ或{x}-[x]=-
+2kπ.
即x=
+2kπ或x=-
+2kπ.
若x=
+2kπ,∵0≤x≤316,
∴当k=0时,x=
,由x=
+2kπ≤316,解得k≤50.3,即k≤50,此时有51个零点,
若x=-
+2kπ,∵0≤x≤316,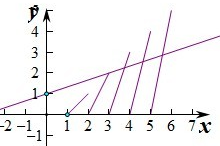
∴当k=0时,x=-
不成立,由x=-
+2kπ≤316,解得k≤50.6,即k≤50,此时有50个零点,
综上f(x)=sin2[x]+sin2{x}-1的零点个数为50+51=101个.
∵{x}=
,
∴[x]{x}=
由g(x)=0得[x]•{x}=
+1,分别作出函数h(x)=[x]{x}和y=
+1的图象如图:
由图象可知当0≤x<1和1≤x<2时,函数h(x)=[x]{x}和y=
+1没有交点,
但2≤x<3时,函数h(x)=[x]{x}和y=
+1在每一个区间上只有一个交点,
∵0≤x<316,
∴g(x)=[x]•{x}-
-1的零点个数为316-2-1=303个.
故m=101,n=303.
故选:A.
则{x}=
| π |
| 2 |
| π |
| 2 |
即{x}-[x]=
| π |
| 2 |
| π |
| 2 |
即x=
| π |
| 2 |
| π |
| 2 |
若x=
| π |
| 2 |
∴当k=0时,x=
| π |
| 2 |
| π |
| 2 |
若x=-
| π |
| 2 |

∴当k=0时,x=-
| π |
| 2 |
| π |
| 2 |
综上f(x)=sin2[x]+sin2{x}-1的零点个数为50+51=101个.
∵{x}=
|
∴[x]{x}=
|
由g(x)=0得[x]•{x}=
| x |
| 3 |
| x |
| 3 |
由图象可知当0≤x<1和1≤x<2时,函数h(x)=[x]{x}和y=
| x |
| 3 |
但2≤x<3时,函数h(x)=[x]{x}和y=
| x |
| 3 |
∵0≤x<316,
∴g(x)=[x]•{x}-
| x |
| 3 |
故m=101,n=303.
故选:A.
点评:本题主要考查函数的新定义题,利用定义作出函数的图象,利用数形结合是解决本题的关键,综合性较强,难度较大.

练习册系列答案
相关题目