题目内容
对于实数x,定义[x]表示不超过x大整数,已知正数数列an满足:a1=1,Sn=
(an+
),其中Sn为数列an的前n项的和,则[
+
+…+
]=( )
| 1 |
| 2 |
| 1 |
| an |
| 1 |
| S1 |
| 1 |
| S2 |
| 1 |
| S100 |
| A、20 | B、19 | C、18 | D、17 |
分析:由题意已知正数数列an满足:a1=1,Sn=
(an+
),利用已知数列的前n项和求其Sn得通项,再求出S=
+
+…+
,利用不等式的性质简单放缩即可.
| 1 |
| 2 |
| 1 |
| an |
| 1 |
| S1 |
| 1 |
| S2 |
| 1 |
| S100 |
解答:解:由于正数数列an满足:a1=1,Sn=
(an+
)=
[(Sn-Sn-1)+
],
?Sn+Sn-1=
?Sn2=Sn-12+1,
因为S1=a1=1,所以,Sn2=n ,由于各项为正项,所以Sn=
,
故
+
<2
<
+
,
=
-
<
<
=
-
,
令S=
+
+…+
,则
>
-1>9?S>18,
又因为S1=a1=1,
所以
=
+…+
<
-1=9,
=1,故s<19,
从而[S]=18.
故选:C
| 1 |
| 2 |
| 1 |
| an |
| 1 |
| 2 |
| 1 |
| Sn-Sn-1 |
?Sn+Sn-1=
| 1 |
| Sn-Sn-1 |
因为S1=a1=1,所以,Sn2=n ,由于各项为正项,所以Sn=
| n |
故
| n |
| n-1 |
| n |
| n+1 |
| n |
| 1 | ||||
|
| n+1 |
| n |
| 1 | ||
2
|
| 1 | ||||
|
| n |
| n-1 |
令S=
| 1 |
| S1 |
| 1 |
| S2 |
| 1 |
| S100 |
| S |
| 2 |
| 101 |
又因为S1=a1=1,
所以
| S |
| 2 |
| 1 |
| 2S2 |
| 1 |
| 2S100 |
| 100 |
| 1 |
| S1 |
从而[S]=18.
故选:C
点评:此题考查了数列的已知数列前n项的和求通项,不等式的性质,不等式的简单放缩,及学生理解题意的能力和计算能力.

练习册系列答案
相关题目
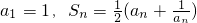 ,其中Sn为数列an的前n项的和,则
,其中Sn为数列an的前n项的和,则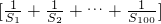 =
=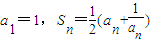 ,其中Sn为数列an的前n项的和,则
,其中Sn为数列an的前n项的和,则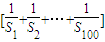 =( )
=( )