题目内容
如果等比数列{an}的首项为正数,公比大于1,那么数列{log
an}( )
| 1 |
| 3 |
| A、是递增的等比数列 |
| B、是递减的等比数列 |
| C、是递增的等差数列 |
| D、是递减的等差数列 |
分析:根据已知中等比数列{an}的首项为正数,公比大于1,我们可以判断{log
an+1}-{log
an}是否为定值,及与0的关系,进而得到答案.
| 1 |
| 3 |
| 1 |
| 3 |
解答:解:∵等比数列{an}的首项为正数,公比大于1,
则可设数列{an}的公比为q,则q>1
则an=a1qn-1,an+1=a1qn,
令bn=log
an,
则bn+1-bn=log
(a1qn)-log
(a1qn-1)=log
q <0
故数列{log
an}是递减的等差数列
故选D
则可设数列{an}的公比为q,则q>1
则an=a1qn-1,an+1=a1qn,
令bn=log
| 1 |
| 3 |
则bn+1-bn=log
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
故数列{log
| 1 |
| 3 |
故选D
点评:本题考查的知识点是等差数列的确定及等比数列的性质,其中根据对数的运算性质,判断{log
an+1}-{log
an}是否为定值,及与0的关系,是解答本题的关键.
| 1 |
| 3 |
| 1 |
| 3 |

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
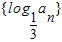 ( )
( )