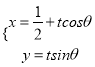题目内容
【题目】将一颗均匀的骰子掷两次,第一次得到的点数记为![]() ,第一次得到的点数记为
,第一次得到的点数记为![]() ,则方程组
,则方程组![]() 有唯一解的概率是___________.
有唯一解的概率是___________.
【答案】![]()
【解析】
所有的可能的结果(a,b)共有6×6=36种,满足直线l1与l2平行的结果(a,b)共有3个,由此求得直线l1与l2平行的概率,用1减去直线l1与l2平行的概率,即得所求.
由题意可知,方程组有唯一解转化为表示方程组![]() 的两直线相交,
的两直线相交,
即直线l1:ax+by=3与直线l2:x+2y=2相交,
又所有的可能出现的结果(a,b)共有6×6=36种,当直线l1与l2平行时,应有![]() ,
,
故其中满足直线l1与直线l2平行的结果(a,b)共有:(1,2)、(2,4)、(3,6),总计3个,故直线l1与l2平行的概率为![]() .又由a,b的意义可知两条直线不重合,
.又由a,b的意义可知两条直线不重合,
故直线l1与l2相交的概率为 1![]() ,
,
∴方程组有唯一解的概率为 1![]() ,
,
故答案为:![]() .
.

练习册系列答案
相关题目