题目内容
【题目】已知两定点![]() 和
和![]() ,动点
,动点![]() 在直线
在直线![]() :
:![]() 上移动,椭圆
上移动,椭圆![]() 以
以![]() ,
,![]() 为焦点且经过点
为焦点且经过点![]() ,则椭圆
,则椭圆![]() 的离心率的最大值为__________.
的离心率的最大值为__________.
【答案】![]()
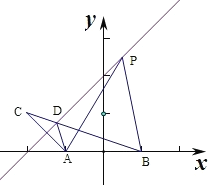
【解析】分析:作出直线y=x+2,过A作直线y=x+2的对称点C,2a=|PA|+|PB|≥|CD|+|DB|=|BC|,即可得到a的最大值,由于c=1,由离心率公式即可得到.
详解:由题意知c=1,离心率e=![]() ,椭圆C以A,B为焦点且经过点P,则c=1,
,椭圆C以A,B为焦点且经过点P,则c=1,
∵P在直线l:y=x+2上移动, ∴2a=|PA|+|PB|.
过A作直线y=x+2的对称点C,
设C(m,n),则由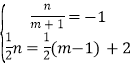 ,
,
解得![]() ,即有C(﹣2,1),
,即有C(﹣2,1),
则此时2a=|PA|+|PB|≥|CD|+|DB|=|BC|=![]() ,此时a有最小值
,此时a有最小值![]() ,
,
对应的离心率e有最大值![]() .
.
故答案为:![]()

练习册系列答案
相关题目
【题目】某研究机构对高三学生的记忆力![]() 和判断力
和判断力![]() 进行统计分析,得下表数据:
进行统计分析,得下表数据:
| 6 | 8 | 10 | 12 |
| 2 | 3 | 5 | 6 |

(1)请在图中画出上表数据的散点图;
(2)请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(3)试根据(2)求出的线性回归方程,预测记忆力为9的同学的判断力.
相关公式: ,
,![]() .
.
【题目】某地西红柿从2月1号起开始上市,通过市场调查,得到西红柿种植成本![]() (单位:元/100
(单位:元/100![]() )与上市时间
)与上市时间![]() (距2月1日的天数,单位:天)的数据如下表:
(距2月1日的天数,单位:天)的数据如下表:
时间 | 50 | 110 | 250 |
成本 | 150 | 108 | 150 |
(1)根据上表数据,从下列函数中选取一个函数描述西红柿种植成本![]() 与上市时间
与上市时间![]() 的变化关系:
的变化关系:![]() ;
;
(2)利用(1)中选取的函数,求西红柿种植成本![]() 最低时的上市天数
最低时的上市天数![]() 及最低种植成本.
及最低种植成本.