题目内容
【题目】4个男同学，3个女同学站成一排.
（1）3个女同学必须排在一起，有多少种不同的排法？
（2）任何两个女同学彼此不相邻，有多少种不同的排法？
（3）甲、乙两人相邻，但都不与丙相邻，有多少种不同的排法？
【答案】（1）720种；（2）1440种；（3）960种.
【解析】
（1）（捆绑法）先让3个女生“捆绑”成一个整体，内部排序，然后把女生看成一个整体，与其余的男生排序；
（2）先把4个男生排列，然后把3个女生向5个空档插孔；
（3）先把甲、乙捆绑成一个整体，再把甲乙这个整体与丙分别插入其余4个元素全排列构成的5个空位中，按分步计数原理求的结果．
（1）（捆绑法）先让3个女生“捆绑”成一个整体，内部排序有
种，然后把女生看成一个整体，与其余的男生排列有
，共有
；
（2）先把4个男生排练有
种排法，然后把3个女生向5个空档插孔，有
；
（3）先甲、乙相邻，再把甲乙这个整体与丙分别插入其余4个元素全排列构成的5个空位中， 按分步计数原理不同的排法有，
（种）．
小学同步三练核心密卷系列答案【题目】某种产品的广告费支出x（单位：百万元）与销售额y（单位：百万元）之间有如下的对应数据：
x | 2 | 4 | 5 | 6 | 8 |
y | 30 | 40 | 60 | 50 | 70 |
（1）画出散点图；
（2）求y关于x的线性回归方程.
（3）如果广告费支出为一千万元，预测销售额大约为多少百万元？
参考公式用最小二乘法求线性回归方程系数公式：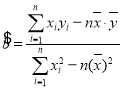
，
.
【题目】某行业主管部门为了解本行业中小企业的生产情况，随机调查了100个企业，得到这些企业第一季度相对于前一年第一季度产值增长率y的频数分布表.
|
|
|
|
|
|
企业数 | 2 | 24 | 53 | 14 | 7 |
（1）分别估计这类企业中产值增长率不低于40%的企业比例、产值负增长的企业比例；
（2）求这类企业产值增长率的平均数与标准差的估计值（同一组中的数据用该组区间的中点值为代表）.（精确到0.01）
附：
.
【题目】推进垃圾分类处理，是落实绿色发展理念的必然选择，也是打赢污染防治攻坚战的重要环节．为了解居民对垃圾分类的了解程度某社区居委会随机抽取1000名社区居民参与问卷测试，并将问卷得分绘制频率分布表如表：
得分 | [30，40） | [40，50） | [50，60） | [60，70） | [70，80） | [80，90） | [90，100] |
男性人数 | 40 | 90 | 120 | 130 | 110 | 60 | 30 |
女性人数 | 20 | 50 | 80 | 110 | 100 | 40 | 20 |
（1）从该社区随机抽取一名居民参与问卷测试试估计其得分不低于60分的概率：
（2）将居民对垃圾分类的了解程度分为“比较了解”（得分不低于60分）和“不太了解”（得分低于60）两类，完成2×2列联表，并判断是否有95%的把握认为“居民对垃圾分类的了解程度”与“性别”有关？
不太了解 | 比较了解 | 合计 | |
男性 | |||
女性 | |||
合计 |
（3）从参与问卷测试且得分不低于80分的居民中，按照性别进行分层抽样，共抽取10人，现从这10人中随机抽取3人作为环保宣传队长，设3人中男性队长的人数为
，求的分布列和期望．
附：
．
临界值表：
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
