题目内容
若0<a<1,0<b<1,把a+b,2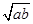 ,2ab中最大与最小者分别记为M和m,则( )
,2ab中最大与最小者分别记为M和m,则( )
| A.M=a+b, m=2ab | B.M=2ab, m=2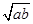 |
C.M=a+b, m=2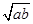 | D.M=2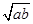 , m=2ab , m=2ab |
A
解析试题分析:因为0<a<1,0<b<1,所以取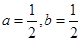 可以验证最大者为a+b,最小者为2ab.
可以验证最大者为a+b,最小者为2ab.
考点:本小题主要考查利用特殊值法判断大小。
点评:解决此类问题时,取特殊值法是常用而且好用的方法.

练习册系列答案
相关题目
关于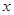 的不等式
的不等式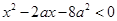 (
( )的解集为
)的解集为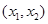 ,且
,且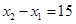 ,则
,则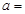 ( )
( )
A. | B. | C.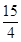 | D.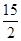 |
在R上定义运算⊙:a⊙b=ab+2a+b,则满足x⊙(x-2)<0的实数x的取值范围为( )
| A.(0,2) | B.(-2,1) |
| C.(-∞,-2)∪(1,+∞) | D.(-1,2) |
已知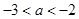 ,
,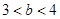 ,则
,则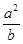 的取值范围为
的取值范围为
A.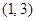 | B. | C.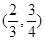 | D. |
不等式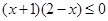 的解集为( )
的解集为( )
A.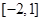 | B.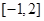 |
C.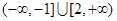 | D.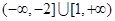 |
若不等式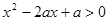 ,对
,对 恒成立,则关于
恒成立,则关于 的不等式
的不等式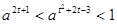 的解集为( )
的解集为( )
A. | B. | C. | D.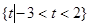 |
关于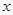 的不等式
的不等式 的解为
的解为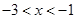 或
或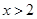 ,则
,则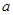 的取值为( )
的取值为( )
| A.2 | B.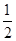 | C.-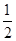 | D.-2 |
如果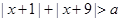 对任意实数x总成立,则a的取值范围是 ( )
对任意实数x总成立,则a的取值范围是 ( )
A. | B. | C. | D.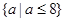 |
若不等式 成立的充分条件是
成立的充分条件是 ,则实数
,则实数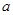 的取值范围是( )
的取值范围是( )
A.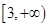 | B. | C. | D.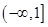 |