题目内容
在R上定义运算⊙:a⊙b=ab+2a+b,则满足x⊙(x-2)<0的实数x的取值范围为( )
| A.(0,2) | B.(-2,1) |
| C.(-∞,-2)∪(1,+∞) | D.(-1,2) |
B
解析试题分析:
解:∵x⊙(x-2)=x(x-2)+2x+x-2<0,∴化简得x2+x-2<0即(x-1)(x+2)<0,得到x-1<0且x+2>0①或x-1>0且x+2<0②,解出①得-2<x<1;解出②得x>1且x<-2无解.∴-2<x<1.故选B
考点:一元二次不等式的解集
点评:此题是一道基础题,要求学生会根据已知的新定义化简求值,会求一元二次不等式的解集

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
不等式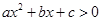 的解集为(-
的解集为(- ,2),则不等式
,2),则不等式 的解集为( )
的解集为( )
A.( ,+∞)∪(-∞,-2) ,+∞)∪(-∞,-2) |
B.(-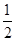 ,+∞)∪(-∞,-3) ,+∞)∪(-∞,-3) |
C.(-2, ) ) |
D.(-3,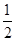 ) ) |
不等式2x -x-1>0的解集是
-x-1>0的解集是
A.( ,1) ,1) |
| B.(1,+∞) |
| C.(-∞,1)∪(2,+∞) |
D.(-∞, )∪(1,+∞) )∪(1,+∞) |
已知点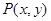 在经过
在经过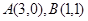 两点的直线上,则
两点的直线上,则 的最小值为( )
的最小值为( )
A.2 | B.4 | C.16 | D.不存在 |
若存在实数 使
使 成立,则实数
成立,则实数 的取值范围是( )
的取值范围是( )
A. | B.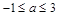 | C. | D. |
函数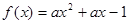 在
在 上满足
上满足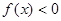 ,则
,则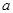 的取值范围是( )
的取值范围是( )
A.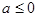 | B.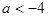 | C.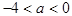 | D.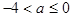 |
设a,b为满足ab<0的实数,那么 ( )
| A.|a+b|>|a-b| | B.|a+b|<|a-b| | C.|a-b|<|a|-|b| | D.|a-b|<|a|+|b| |
若0<a<1,0<b<1,把a+b,2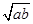 ,2ab中最大与最小者分别记为M和m,则( )
,2ab中最大与最小者分别记为M和m,则( )
| A.M=a+b, m=2ab | B.M=2ab, m=2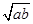 |
C.M=a+b, m=2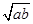 | D.M=2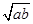 , m=2ab , m=2ab |
不等式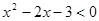 的解集为
的解集为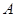 ,不等式
,不等式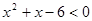 的解集为
的解集为 ,不等式
,不等式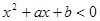 的解集是
的解集是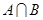 ,那么
,那么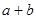 等于 ( )
等于 ( )
| A.-3 | B.1 | C.-1 | D.3 |