题目内容
12. 在棱长为1的正方体ABCD-A1B1C1D1中,E为DD1的中点.
在棱长为1的正方体ABCD-A1B1C1D1中,E为DD1的中点.(1)求二面角B1-AC-E的大小;
(2)求点B到平面AEC的距离.
分析 (1)取AC的中点O,连接EO,B1O,B1E,则EO⊥AC,B1O⊥AC,∠B1OE是二面角B1-AC-E的平面角,即可求二面角B1-AC-E的大小;
(2)由等体积可求点B到平面AEC的距离.
解答 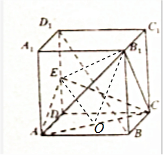 解:(1)取AC的中点O,连接EO,B1O,B1E,则EO⊥AC,B1O⊥AC,
解:(1)取AC的中点O,连接EO,B1O,B1E,则EO⊥AC,B1O⊥AC,
∴∠B1OE是二面角B1-AC-E的平面角,
∵EO=$\frac{\sqrt{3}}{2}$,B1O=$\frac{\sqrt{6}}{2}$,B1E=$\frac{3}{2}$,
∴cos∠B1OE=$\frac{\frac{3}{4}+\frac{6}{4}-\frac{9}{4}}{2×\frac{\sqrt{3}}{2}×\frac{\sqrt{6}}{2}}$=0,
∴∠B1OE=90°,即二面角B1-AC-E的平面角是90°;
(2)设点B到平面AEC的距离为h,则
∵S△AEC=$\frac{1}{2}×\sqrt{2}×\frac{\sqrt{3}}{2}$=$\frac{\sqrt{6}}{4}$,S△ABC=$\frac{1}{2}$,
∴由等体积可得,$\frac{1}{3}$•S△ABC•ED=$\frac{1}{3}$S△AEC•h,即$\frac{1}{3}×\frac{1}{2}×\frac{1}{2}=\frac{1}{3}×\frac{\sqrt{6}}{4}h$,
∴h=$\frac{\sqrt{6}}{6}$.
点评 本题考查二面角平面角的计算,考查点面距离的计算,考查学生分析解决问题的能力,确定二面角的平面角,正确运用等体积法是关键.

练习册系列答案
相关题目
2.如图程序运行后,输出的值是( )


| A. | -4 | B. | 5 | C. | 9 | D. | 14 |
 在长方体ABCD-A1B1C1D1中,AA1=9,AB=BC=6$\sqrt{3}$,N,M,P分别为BC,A1B1,C1D1的中点.
在长方体ABCD-A1B1C1D1中,AA1=9,AB=BC=6$\sqrt{3}$,N,M,P分别为BC,A1B1,C1D1的中点. 如图,M是Rt△ABC与Rt△ABD的公共边AB的中点,连结CM,DM,恰好△CMD为直角三角形,若BD=6,AD=8,求CD的长.
如图,M是Rt△ABC与Rt△ABD的公共边AB的中点,连结CM,DM,恰好△CMD为直角三角形,若BD=6,AD=8,求CD的长. 如图,在四面体P-ABC中,底面ABC是边长为1的正三角形,PB=PC=$\sqrt{2}$,AB⊥BP.
如图,在四面体P-ABC中,底面ABC是边长为1的正三角形,PB=PC=$\sqrt{2}$,AB⊥BP.