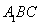题目内容
如图,在几何体ABCDE中,△ABC是等腰直角三角形,![]() ,BE和CD都垂直于平面ABC,且BE=AB=2,CD=1,点F是AE的中点。
,BE和CD都垂直于平面ABC,且BE=AB=2,CD=1,点F是AE的中点。

(1)证明:DF∥平面ABC;
(2)求AB与平BDF所成角的大小。
解:(1)取AB的中点G,连CG,GF,如图a所示。

则GF∥BE,且![]() ,
,
∴GF∥CD,且GF=CD。
∴四边形FGCD是平行四边形。
∴GF∥CG,又![]() 平面ABC,
平面ABC,![]() 平面ABC,
平面ABC,
∴DF∥平面ABC。
(2)解法一:设A到平面BDF的距离为![]() ,
,
由![]() 得
得![]()
在![]() 中,
中,![]() ,
,
∴![]() ,又
,又![]() ,且
,且![]() ,
,
∴
又设AB与平面BDF所成的角为![]() ,则
,则 ,
,
故AB与平面BDF所成的角为![]() 。
。
解法二:以点B为原点,BA、BC、BE所在的直线分别为![]() 、
、![]() 、
、![]() 轴,
轴,
建立如图b所示的空间直角坐标

系,则B(0,0,0),A(2,0,0),C(0,2,0),D(0,2,1),
E(0,0,2),F(1,0,1).
![]()
设平面BDF的一个法向量为![]() ,
,
∵![]()
∴
即![]() ,解得
,解得![]()
∴![]() 。
。
又设AB与平面BDF所成的角为![]() ,则法线
,则法线![]() 与
与![]() 所成的角为
所成的角为![]() ,
,
∴ ,即
,即![]()
故AB与平面BDF所成的角为![]() 。
。

练习册系列答案
相关题目
 如图,在几何体ABCDE中,△ABC是等腰直角三角形,∠ABC=90°,BE和CD都垂直于平面ABC,且BE=AB=2,CD=1,点F是AE的中点.
如图,在几何体ABCDE中,△ABC是等腰直角三角形,∠ABC=90°,BE和CD都垂直于平面ABC,且BE=AB=2,CD=1,点F是AE的中点. 如图,在几何体ABCDE中,△ABC是等腰直角三角形,∠ABC=90°,BE和CD都垂直于平面ABC,且BE=AB=2,CD=1,F是AE的中点.
如图,在几何体ABCDE中,△ABC是等腰直角三角形,∠ABC=90°,BE和CD都垂直于平面ABC,且BE=AB=2,CD=1,F是AE的中点. (2012•合肥一模)如图,在多面体ABC-A1B1C1中,AA1⊥平面ABC,AA1⊥平面ABC,AA1∥=BB1,AB=AC=AA1=
(2012•合肥一模)如图,在多面体ABC-A1B1C1中,AA1⊥平面ABC,AA1⊥平面ABC,AA1∥=BB1,AB=AC=AA1=