题目内容
按要求证明下列各题．
（1）已知a1+a2+a3+a4＞100，用反证法证明a1，a2，a3，a4中，至少有一个数大于25；
（2）已知a，b是不相等的正数．用分析法证明a3+b3＞a2b+ab2．
证明：（1）假设a1，a2，a3，a4均不大于25，…（2分）
那么，a1+a2+a3+a4≤25+25+25+25=100，这与已知条件矛盾．
所以，a1，a2，a3，a4中，至少有一个数大于25． …（6分）
（2）要证明a3+b3＞a2b+ab2，只需证明（a+b）（a2-ab+b2）＞ab（a+b），
只需证明（a+b）（a2-ab+b2）-ab（a+b）＞0，
只需证明（a+b）（a2-2ab+b2）＞0，
只需证明（a+b）（a-b）2＞0．…（11分）
∵a，b是不相等的正数，∴a+b＞0，（a-b）2＞0成立，…（13分）
这样，就证明了命题的结论成立．…（15分）
分析：（1）假设a1，a2，a3，a4均不大于25，则得a1+a2+a3+a4≤25+25+25+25=100，这与已知条件矛盾，故假设不对．
故要证的结论成立．
（2）要证明不等式成立，只需证明（a+b）（a2-ab+b2）-ab（a+b）＞0，即证（a+b）（a-b）2＞0，由a，b是不相等的正数，可得+b＞0，（a-b）2＞0成立，从而，原不等式成立．
点评：本题主要考查用反证法证明数学命题，用分析法证明不等式成立，属于中档题．
那么，a1+a2+a3+a4≤25+25+25+25=100，这与已知条件矛盾．
所以，a1，a2，a3，a4中，至少有一个数大于25． …（6分）
（2）要证明a3+b3＞a2b+ab2，只需证明（a+b）（a2-ab+b2）＞ab（a+b），
只需证明（a+b）（a2-ab+b2）-ab（a+b）＞0，
只需证明（a+b）（a2-2ab+b2）＞0，
只需证明（a+b）（a-b）2＞0．…（11分）
∵a，b是不相等的正数，∴a+b＞0，（a-b）2＞0成立，…（13分）
这样，就证明了命题的结论成立．…（15分）
分析：（1）假设a1，a2，a3，a4均不大于25，则得a1+a2+a3+a4≤25+25+25+25=100，这与已知条件矛盾，故假设不对．
故要证的结论成立．
（2）要证明不等式成立，只需证明（a+b）（a2-ab+b2）-ab（a+b）＞0，即证（a+b）（a-b）2＞0，由a，b是不相等的正数，可得+b＞0，（a-b）2＞0成立，从而，原不等式成立．
点评：本题主要考查用反证法证明数学命题，用分析法证明不等式成立，属于中档题．
练习册系列答案
捷径训练检测卷系列答案
小夫子全能检测系列答案
相关题目
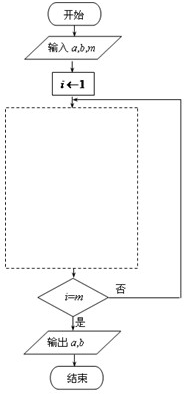若数列{an}，{bn}中，a1=a，b1=b，
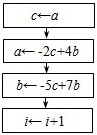B、
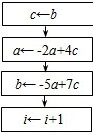
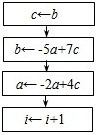D、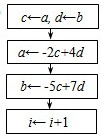
，
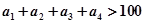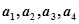中，至少有一个数大于25 
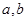是不相等的正数.用分析法证明
.
，
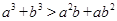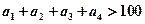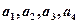中，至少有一个数大于25 
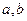是不相等的正数.用分析法证明
.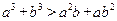