题目内容
下列结论:
①已知命题p:∃x∈R,tanx=1;命题q:∀x∈R,x2﹣x+1>0.则命题“p∧¬q”是假命题;
②函数![]() 的最小值为
的最小值为![]() 且它的图象关于y轴对称;
且它的图象关于y轴对称;
③“a>b”是“2a>2b”的充分不必要条件;
④在△ABC中,若sinAcosB=sinC,则△ABC中是直角三角形.
⑤若![]() ;
;
其中正确命题的序号为 .(把你认为正确的命题序号填在横线处)
考点:
命题的真假判断与应用.
专题:
计算题;函数的性质及应用;三角函数的图像与性质.
分析:
①由命题p:∃x∈R,tanx=1是真命题;命题q:∀x∈R,x2﹣x+1>0是真命题.知命题“p∧¬q”是假命题;②当x=0时,![]() =0;③“a>b”是“2a>2b”充要条件;④在△ABC中,由sinAcosB=sinC,知a2=b2+c2;⑤tanθ=2,知sin2θ=2sinθcosθ=2×
=0;③“a>b”是“2a>2b”充要条件;④在△ABC中,由sinAcosB=sinC,知a2=b2+c2;⑤tanθ=2,知sin2θ=2sinθcosθ=2×![]() =
=![]() .
.
解答:
解:①∵命题p:∃x∈R,tanx=1是真命题;命题q:∀x∈R,x2﹣x+1>0是真命题.
∴命题“p∧¬q”是假命题,故①正确;
②当x=0时,![]() =0,故②错误;
=0,故②错误;
③∵“a>b”⇔“2a>2b”,
∴“a>b”是“2a>2b”充要条件,故③错误;
④在△ABC中,∵sinAcosB=sinC,
∴a•![]() =c,
=c,
∴a2=b2+c2,
∴△ABC中是直角三角形.故④正确;
⑤∵tanθ=2,
∴sin2θ=2sinθcosθ=2×![]() =
=![]() ,故⑤正确.
,故⑤正确.
故答案为:①④⑤.
点评:
本题考查命题的真假判断,是基础题.解题时要注意不等式和三角函数等知识点的合理运用.

练习册系列答案
相关题目
已知命p:?x∈R,使得x+
<2,命题q:?x∈R,x2+x+1>0,下列结论正确的是( )
| 1 |
| x |
| A、命题“p∧q”是真命题 |
| B、命题“(¬p)∧q”是真命题 |
| C、命题“p∧(¬q)”是真命题 |
| D、命题“(¬p)∧(¬q)”是真命题 |
 ,命题q:?x∈R,x2+x+1>0,下列结论正确的是( )
,命题q:?x∈R,x2+x+1>0,下列结论正确的是( )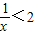 ,命题q:?x∈R,x2+x+1>0,下列结论正确的是( )
,命题q:?x∈R,x2+x+1>0,下列结论正确的是( )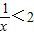 ,命题q:?x∈R,x2+x+1>0,下列结论正确的是( )
,命题q:?x∈R,x2+x+1>0,下列结论正确的是( )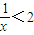 ,命题q:?x∈R,x2+x+1>0,下列结论正确的是( )
,命题q:?x∈R,x2+x+1>0,下列结论正确的是( )