题目内容
已知命p:?x∈R,使得x+
<2,命题q:?x∈R,x2+x+1>0,下列结论正确的是( )
| 1 |
| x |
| A、命题“p∧q”是真命题 |
| B、命题“(¬p)∧q”是真命题 |
| C、命题“p∧(¬q)”是真命题 |
| D、命题“(¬p)∧(¬q)”是真命题 |
分析:先解出这两个命题对应的不等式,得到这两个命题都是真命题,对于这两个真命题,得到用且连接的符合命题是真命题.
解答:解:∵命p:?x∈R,使得x+
<2,解这个不等式的x<0,
∴存在x∈R,使得x+
<2,故本命题正确,
命题q:?x∈R,x2+x+1>0,
∵x2+x+1>0等价于(x+
)2+
>0
∴?x∈R,x2+x+1>0,正确,
所给的两个命题都正确,
∴命题“p∧q”是真命题
故选A.
| 1 |
| x |
∴存在x∈R,使得x+
| 1 |
| x |
命题q:?x∈R,x2+x+1>0,
∵x2+x+1>0等价于(x+
| 1 |
| 2 |
| 3 |
| 4 |
∴?x∈R,x2+x+1>0,正确,
所给的两个命题都正确,
∴命题“p∧q”是真命题
故选A.
点评:本题考查符合命题的真假,考查不等式的解法,考查全称命题和特称命题,是一个基础题,这种题目可以出现在大型考试的选择或填空中,是一个必得分题目.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ,命题q:?x∈R,x2+x+1>0,下列结论正确的是( )
,命题q:?x∈R,x2+x+1>0,下列结论正确的是( ) ,命题q:?x∈R,x2+x+1>0,下列结论正确的是( )
,命题q:?x∈R,x2+x+1>0,下列结论正确的是( )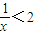 ,命题q:?x∈R,x2+x+1>0,下列结论正确的是( )
,命题q:?x∈R,x2+x+1>0,下列结论正确的是( )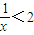 ,命题q:?x∈R,x2+x+1>0,下列结论正确的是( )
,命题q:?x∈R,x2+x+1>0,下列结论正确的是( )