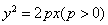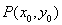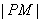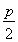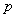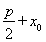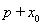题目内容
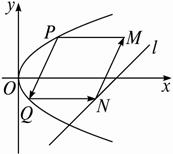
抛物线有光学性质:由其焦点射出的光线经抛物线反象后,沿平行于抛物线对称轴的肖向射出,反之亦然.如图所示,今有抛物线C,其顶点是坐标原点,对称辅为x轴.开口向右.一光源在点M处,由其发出一条平行于x轴的光线射向抛物线C卜的点P(4.4),经抛物线C反射后,反射光线经过焦点F后射向抛物线C上的点Q,再经抛物线C反射后又沿平行于X轴的方向射出,途中经直线l:2x-4y-17=0上点N反射后又射回点M.(1)求抛物线C的方程;
(2)求PQ的长度;
(3)判断四边形MPQN是否为平行四边形,若是请给出证明,若不是请说明理由.

【答案】分析:(1)设抛物线方程为y2=2px,将P (4,4)代入可得抛物线方程;
(2)确定直线PF方程,代入抛物线方程,求出Q的坐标,即可求PQ的长度;
(3)求出M的坐标,证明MN的斜率与PQ的斜率相等,即可得到结论.
解答: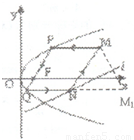 解:(1)设抛物线方程为y2=2px,将P (4,4)代入可得p=2,故抛物线方程为y2=4x,…(4分)
解:(1)设抛物线方程为y2=2px,将P (4,4)代入可得p=2,故抛物线方程为y2=4x,…(4分)
(2)由y2=4x可得F(1,0),则直线PF方程为:y= (x-1)
(x-1)
即x=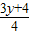 代入y2=4x,得y2=3y+4解得y=4或-1,
代入y2=4x,得y2=3y+4解得y=4或-1,
故Q的纵坐标为-l,可得Q( ,-1),故|PQ|=
,-1),故|PQ|=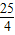 …(5分)
…(5分)
(3)四边形MPQN是平行四边形 …(1分)
下面证明:先求出M的坐标,M的纵坐标为4,故设M(x,4),
由光线性质知M关于直线的对称点M1在直线QN上,故M1(x1,-1),
则MM1中点(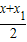 ,
, )在直线上,且MM斜率为-2,得x+x1-6-17=0,
)在直线上,且MM斜率为-2,得x+x1-6-17=0,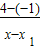 =-2,
=-2,
解得:M(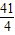 ,4),
,4),
所以N(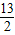 ,-1)
,-1)
所以MN的斜率为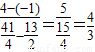 ,与PQ斜率相等,
,与PQ斜率相等,
故MN∥PQ,又MP∥QN,故四边形MPQN是平行四边形.…(4分)
点评:本题考查抛物线方程,考查两点间的距离公式,考查学生分析解决问题的能力,属于中档题.
(2)确定直线PF方程,代入抛物线方程,求出Q的坐标,即可求PQ的长度;
(3)求出M的坐标,证明MN的斜率与PQ的斜率相等,即可得到结论.
解答:
 解:(1)设抛物线方程为y2=2px,将P (4,4)代入可得p=2,故抛物线方程为y2=4x,…(4分)
解:(1)设抛物线方程为y2=2px,将P (4,4)代入可得p=2,故抛物线方程为y2=4x,…(4分)(2)由y2=4x可得F(1,0),则直线PF方程为:y=
 (x-1)
(x-1)即x=
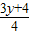 代入y2=4x,得y2=3y+4解得y=4或-1,
代入y2=4x,得y2=3y+4解得y=4或-1,故Q的纵坐标为-l,可得Q(
 ,-1),故|PQ|=
,-1),故|PQ|=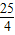 …(5分)
…(5分)(3)四边形MPQN是平行四边形 …(1分)
下面证明:先求出M的坐标,M的纵坐标为4,故设M(x,4),
由光线性质知M关于直线的对称点M1在直线QN上,故M1(x1,-1),
则MM1中点(
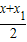 ,
, )在直线上,且MM斜率为-2,得x+x1-6-17=0,
)在直线上,且MM斜率为-2,得x+x1-6-17=0,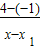 =-2,
=-2,解得:M(
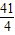 ,4),
,4),所以N(
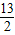 ,-1)
,-1)所以MN的斜率为
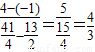 ,与PQ斜率相等,
,与PQ斜率相等,故MN∥PQ,又MP∥QN,故四边形MPQN是平行四边形.…(4分)
点评:本题考查抛物线方程,考查两点间的距离公式,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
 抛物线有光学性质:由其焦点射出的光线经抛物线反象后,沿平行于抛物线对称轴的肖向射出,反之亦然.如图所示,今有抛物线C,其顶点是坐标原点,对称辅为x轴.开口向右.一光源在点M处,由其发出一条平行于x轴的光线射向抛物线C卜的点P(4.4),经抛物线C反射后,反射光线经过焦点F后射向抛物线C上的点Q,再经抛物线C反射后又沿平行于X轴的方向射出,途中经直线l:2x-4y-17=0上点N反射后又射回点M.
抛物线有光学性质:由其焦点射出的光线经抛物线反象后,沿平行于抛物线对称轴的肖向射出,反之亦然.如图所示,今有抛物线C,其顶点是坐标原点,对称辅为x轴.开口向右.一光源在点M处,由其发出一条平行于x轴的光线射向抛物线C卜的点P(4.4),经抛物线C反射后,反射光线经过焦点F后射向抛物线C上的点Q,再经抛物线C反射后又沿平行于X轴的方向射出,途中经直线l:2x-4y-17=0上点N反射后又射回点M.