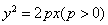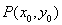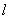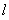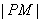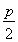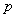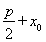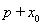题目内容
抛物线有光学性质:由其焦点射出的光线经抛物线折射后,沿平行于抛物线对称轴的方向射出.今有抛物线y2=2px(p>0),一光源在点M(
(1)设P、Q两点的坐标分别为(x1,y1),(x2,y2),证明:y1y2=-p2;
(2)求抛物线的方程;
(3)试判断在抛物线上是否存在一点,使该点与点M关于PN所在的直线对称?若存在,请求出此点的坐标;若不存在,请说明理由.
答案:(1)证明:由抛物线的光学性质及题意知,光线PQ必过抛物线的焦点(![]() ,0),设直线方程为y=k(x-
,0),设直线方程为y=k(x-![]() ).
).
由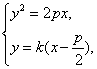
得y2-![]() y-p2=0.
y-p2=0.
由韦达定理得y1y2=-p2.
当直线PQ的斜率不存在时,x=![]() ,y1y2=-p2也成立.
,y1y2=-p2也成立.
(2)解:因为光线QN经直线l反射后又射向M点,所以直线MN与直线QN关于直线l对称,设M(![]() ,4)关于直线l的对称点为M′(x′,y′),则
,4)关于直线l的对称点为M′(x′,y′),则
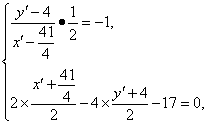
解之,得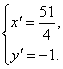
所以直线QN的方程为y=-1,Q点的纵坐标为y2=-1,由题意知P点的纵坐标y1=4.由(1)的结论知y1y2=-p2,即p2=4,p=2.
所以抛物线方程为y2=4x.
(3)解:P点的坐标为P(4,4),
由![]()
解得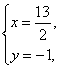 即N(
即N(![]() ,-1).
,-1).
所以直线PN的方程为2x+y-12=0.
设M点关于直线PN的对称点为M1(x1,y1),则
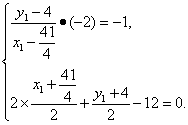
解之,得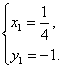
M1(![]() ,-1)的坐标是抛物线y2=4x的解,故抛物线上存在一点(
,-1)的坐标是抛物线y2=4x的解,故抛物线上存在一点(![]() ,-1)与点M关于直线PN对称.
,-1)与点M关于直线PN对称.

练习册系列答案
 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
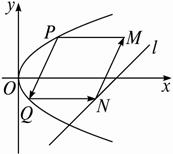
 抛物线有光学性质:由其焦点射出的光线经抛物线反象后,沿平行于抛物线对称轴的肖向射出,反之亦然.如图所示,今有抛物线C,其顶点是坐标原点,对称辅为x轴.开口向右.一光源在点M处,由其发出一条平行于x轴的光线射向抛物线C卜的点P(4.4),经抛物线C反射后,反射光线经过焦点F后射向抛物线C上的点Q,再经抛物线C反射后又沿平行于X轴的方向射出,途中经直线l:2x-4y-17=0上点N反射后又射回点M.
抛物线有光学性质:由其焦点射出的光线经抛物线反象后,沿平行于抛物线对称轴的肖向射出,反之亦然.如图所示,今有抛物线C,其顶点是坐标原点,对称辅为x轴.开口向右.一光源在点M处,由其发出一条平行于x轴的光线射向抛物线C卜的点P(4.4),经抛物线C反射后,反射光线经过焦点F后射向抛物线C上的点Q,再经抛物线C反射后又沿平行于X轴的方向射出,途中经直线l:2x-4y-17=0上点N反射后又射回点M.