题目内容
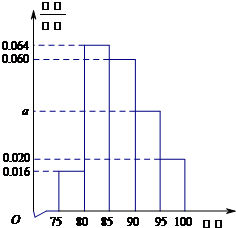 (2013•昌平区二模)某高校在2013年的自主招生考试成绩中随机抽取50名学生的笔试成绩,绘制成频率分布直方图如图所示,由图中数据可知a=
(2013•昌平区二模)某高校在2013年的自主招生考试成绩中随机抽取50名学生的笔试成绩,绘制成频率分布直方图如图所示,由图中数据可知a=0.040
0.040
;若要从成绩在[85,90),[90,95),[95,100]三组内的学生中,用分层抽样的方法选取12人参加面试,则成绩在[95,100]内的学生中,学生甲被选取的概率为| 2 |
| 5 |
| 2 |
| 5 |
分析:根据频率分步直方图的性质可以知道,所有小正方形的面积之和等于各组的频率之和是1,列出四个小正方形的面积之和,得到关于a的方程,解方程即可;求出第3、4、5组共有12名学生,所以利用分层抽样在50名学生中抽取12名学生,得到第3、4、5组分别抽取的人数,由此能求出成绩在[95,100]内的学生中,学生甲被选取的概率.
解答:解:由频率分步直方图知,
(0.016+0.064+0.06+a+0.02)×5=1,
∴a=0.040.
第3组的人数为0.060×5×50=15,
第4组的人数为0.040×5×50=10.…(2分)
第5组的人数为0.020×5×50=5,
因为第3、4、5组共抽30名学生,
所以利用分层抽样在30名学生中抽取12名学生(3分)
每组抽取的人数分别为:
第3组:
×12=6,
第4组:
×12=4,
第5组:
×12=2,
所以第3、4、5组分别抽取6人、4人、2人.…(5分)
则成绩在[95,100]内的5个学生中抽2个,学生甲被选取的概率为
.
故答案为:0.040;
.
(0.016+0.064+0.06+a+0.02)×5=1,
∴a=0.040.
第3组的人数为0.060×5×50=15,
第4组的人数为0.040×5×50=10.…(2分)
第5组的人数为0.020×5×50=5,
因为第3、4、5组共抽30名学生,
所以利用分层抽样在30名学生中抽取12名学生(3分)
每组抽取的人数分别为:
第3组:
| 15 |
| 30 |
第4组:
| 10 |
| 30 |
第5组:
| 5 |
| 30 |
所以第3、4、5组分别抽取6人、4人、2人.…(5分)
则成绩在[95,100]内的5个学生中抽2个,学生甲被选取的概率为
| 2 |
| 5 |
故答案为:0.040;
| 2 |
| 5 |
点评:本题考查用样本的频率分布估计总体的分布,考查频率分步直方图的性质,考查频率、频数和样本容量之间的关系,本题是一个基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2013•昌平区二模)如图,在边长为2的菱形ABCD中,∠BAD=60°,E为CD的中点,则
(2013•昌平区二模)如图,在边长为2的菱形ABCD中,∠BAD=60°,E为CD的中点,则