题目内容
下列几个命题:
①方程 有一个正实根,一个负实根,则a<0;
有一个正实根,一个负实根,则a<0;
②函数 是偶函数,但不是奇函数;
是偶函数,但不是奇函数;
③函数 的定义域是[-2,2],则函数
的定义域是[-2,2],则函数 的定义域为[-1,3];
的定义域为[-1,3];
④一条曲线 和直线y=a(a
和直线y=a(a )的公共点个数是m,则m的值不可能是1.其中真命题的个数是
)的公共点个数是m,则m的值不可能是1.其中真命题的个数是
| A.1 | B.2 | C.3 | D.4 |
B
解析试题分析:对于①∵方程 的有一个正实根,一个负实根,则
的有一个正实根,一个负实根,则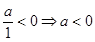 ,因此正确;对于②要使函数
,因此正确;对于②要使函数 有意义,则
有意义,则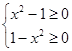 ,解得
,解得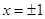 ,因此y=0(
,因此y=0(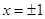 ),故函数既是偶函数,又是奇函数,故不正确;对于③函数
),故函数既是偶函数,又是奇函数,故不正确;对于③函数 的定义域是[-2,2],则函数
的定义域是[-2,2],则函数 的定义域为[-3,1],故不正确;对于④一条曲线
的定义域为[-3,1],故不正确;对于④一条曲线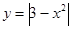 和直线y=a(a
和直线y=a(a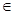 R)的有公共点,则|3-x2|=a≥0,∴x2-3=
R)的有公共点,则|3-x2|=a≥0,∴x2-3=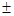 a,即x2=3±a>0,∴x=±
a,即x2=3±a>0,∴x=±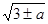 ,因此公共点的个数m可以是2,4,故m的值不可能是1.综上可知:其中正确的有 ①④,故选B.
,因此公共点的个数m可以是2,4,故m的值不可能是1.综上可知:其中正确的有 ①④,故选B.
考点:命题真假的判断与应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知函数f(x)是偶函数,在 上导数
上导数 >0恒成立,则下列不等式成立的是( ).
>0恒成立,则下列不等式成立的是( ).
| A.f(-3)<f(-1)<f(2) | B.f(-1)<f(2)<f(-3) |
| C.f(2)<f(-3)<f(-1) | D.f(2)<f(-1)<f(-3) |
已知奇函数f (x)和偶函数g(x)分别满足  ,
,  ,若存在实数a,使得
,若存在实数a,使得  成立,则实数b的取值范围是
成立,则实数b的取值范围是
| A.(-1,1) | B. | C. | D. |
已知函数 的图像如图所示,则
的图像如图所示,则 的取值范围是( )
的取值范围是( )
A. | B. | C. | D. |
定义在R上的函数 具有下列性质:①
具有下列性质:① ;②
;② ;③
;③ 在
在 上为增函数,则对于下述命题:
上为增函数,则对于下述命题:
① 为周期函数且最小正周期为4;
为周期函数且最小正周期为4;
② 的图像关于
的图像关于 轴对称且对称轴只有1条;
轴对称且对称轴只有1条;
③ 在
在 上为减函数.
上为减函数.
正确命题的个数为( )
| A.0个 | B.1个 | C.2个 | D.3个 |
函数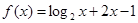 的零点必落在区间( )
的零点必落在区间( )
A.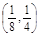 | B.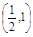 | C.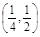 | D.(1,2) |
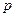 :实数
:实数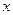 满足
满足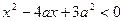 ,其中
,其中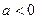 ;
;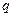 :实数
:实数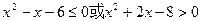 ,且
,且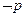 是
是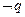 的必要不充分条件,求
的必要不充分条件,求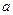 的取值范围。
的取值范围。 的必要不充分条件,求a的取值范围.
的必要不充分条件,求a的取值范围. 的图象可能是( )
的图象可能是( )