题目内容
11.已知三棱锥P-ABC的外接球的球心O在AB上,且PO⊥平面ABC,2AC=$\sqrt{3}$AB,若三棱锥P-ABC的体积为$\frac{3}{2}$,则该三棱锥的外接球的体积为( )| A. | 8$\sqrt{3}$π | B. | 6$\sqrt{3}$π | C. | 4$\sqrt{3}$π | D. | 2$\sqrt{3}$π |
分析 如图所示,由于三棱锥P-ABC的外接球的球心O在AB上,且PO⊥平面ABC,可得PO是三棱锥P-ABC的高,OA=OB=OC=OP=x,AC⊥BC.而2AC=$\sqrt{3}$AB,可得BC=x,AC=$\sqrt{3}$x.利用三棱锥的体积计算公式可得x,再利用球的体积计算公式即可得出.
解答 解:如图所示,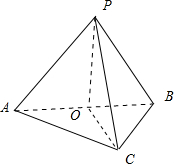
∵三棱锥P-ABC的外接球的球心O在AB上,且PO⊥平面ABC,
∴PO是三棱锥P-ABC的高,OA=OB=OC=OP=x,
∴∠ACB=90°,
∴AC⊥BC.
∵2AC=$\sqrt{3}$AB,
∴∠ABC=60°,
∴BC=x,AC=$\sqrt{3}$x.
∴VP-ABC=$\frac{1}{3}•{S}_{△ABC}•PO$=$\frac{1}{3}×\frac{1}{2}×\sqrt{3}{x}^{2}×x$=$\frac{3}{2}$,
解得x=$\sqrt{3}$.
∴该三棱锥的外接球的体积V=$\frac{4π}{3}{x}^{3}$=$4\sqrt{3}π$.
故选:C.
点评 本题考查了线面垂直的性质、三棱锥的体积计算公式、球的体积计算公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案
相关题目
19.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)与抛物线y2=8x有一个共同的焦点F,且两曲线的一个交点为P,若|PF|=5,则点F到双曲线的渐进线的距离为( )
| A. | $\sqrt{3}$ | B. | 2 | C. | $\sqrt{6}$ | D. | 3 |
1.已知{an}为各项都是正数的等比数列,若a4•a8=4,则a5•a6•a7=( )
| A. | 4 | B. | 8 | C. | 16 | D. | 64 |