题目内容
【题目】如图，直角三角形ABC的顶点坐标A（﹣2，0），直角顶点 
，顶点C在x轴上，点P为线段OA的中点． （Ⅰ）求BC边所在直线方程；
（Ⅱ）圆M是△ABC的外接圆，求圆M的方程．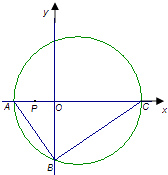
【答案】解：（Ⅰ）∵ 
， ∴ 
；
∴直线BC的方程是y= 
x﹣2 
﹒
（Ⅱ）由（Ⅰ）可得C（4，0），
∴圆心M（1，0），
∴圆M的方程是：（x﹣1）2+y2=9
【解析】（Ⅰ）求出 
，运用直线方程的点斜式列式，再化简即可得到直线BC方程；（Ⅱ）根据A、C两点的坐标算出AC中点M坐标为（1，0），而圆M的半径R= 
|AC|=3，利用圆方程的标准形式即可写出圆M的方程为（x﹣1）2+y2=9．
【考点精析】关于本题考查的圆的标准方程，需要了解圆的标准方程：
；圆心为A(a,b),半径为r的圆的方程才能得出正确答案．
练习册系列答案
相关题目
