题目内容
6.已知函数f(x)=x2ex对区间(a,a+1)内存在极值点,则实数a的取值范围是( )| A. | (-3,-1)∪(0,2) | B. | (-3,-2)∪(-1,0) | C. | (-2,-1)∪(0,3) | D. | (-3,-2)∪(0,1) |
分析 通过求导函数,函数的极值点,利用函数f(x)=x2ex在区间(a,a+1)上存在极值点,建立不等式,即可求实数a的取值范围.
解答 解:函数f(x)=x2ex的导数为y′=2xex+x2ex =xex(x+2),
令y′=0,则x=0或-2,
-2<x<0上单调递减,(-∞,-2),(0,+∞)上单调递增,
∴0或-2是函数的极值点,
∵函数f(x)=x2ex在区间(a,a+1)上存在极值点,
∴a<-2<a+1或a<0<a+1,
∴-3<a<-2或-1<a<0.
实数a的取值范围是:(-3,-2)∪(-1,0).
故选:B.
点评 本题主要考查利用导数研究函数的单调性,考查函数的极值,考查学生的计算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.如图所示的程序框图,若输出的S=63,则判断框内填入的条件是( )
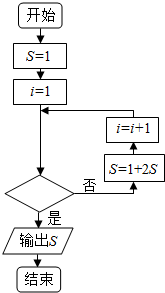

| A. | i>5? | B. | i>6? | C. | i≤5? | D. | i≤6? |
 如图,已知三角形ABC面积为3cm2,BD=3AB,AF=3AC,EC=4BC,那么三角形DEF的面积是多少?
如图,已知三角形ABC面积为3cm2,BD=3AB,AF=3AC,EC=4BC,那么三角形DEF的面积是多少?