题目内容
1. 如图,已知三角形ABC面积为3cm2,BD=3AB,AF=3AC,EC=4BC,那么三角形DEF的面积是多少?
如图,已知三角形ABC面积为3cm2,BD=3AB,AF=3AC,EC=4BC,那么三角形DEF的面积是多少?
分析 连结CD、BF,由已知得S△ACD=2S△ABC,S△DBE=3S△BDC,S△DCF=2S△ACD,S△BCF=2S△ABC,S△BEF=3S△BCF,由此能求出三角形DEF的面积.
解答 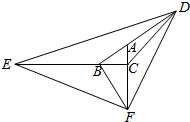 解:连结CD、BF,
解:连结CD、BF,
∵三角形ABC面积为3cm2,BD=3AB,AF=3AC,EC=4BC,
∴S△ACD=2S△ABC=6cm2,S△DBE=3S△BDC=3(3+6)=27(cm2),
S△DCF=2S△ACD=12cm2,S△BCF=2S△ABC=6cm2,
S△BEF=3S△BCF=18cm2,
∴S△DEF=S△ACD+S△ABC+S△DBE+S△DCF+S△BCF+S△BEF=6+3+27+12+6+18=72cm2.
∴三角形DEF的面积是72cm2.
点评 本题考查三角形面积的求法,是中档题,解题时要认真审题,注意三角形面积公式及性质的合理运用.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案
相关题目
18.下列函数在(0,+∞)上是增函数的是( )
| A. | y=9-x2 | B. | y=|x-1| | C. | y=($\frac{1}{2}$)x | D. | y=x${\;}^{\frac{1}{2}}$ |
6.已知函数f(x)=x2ex对区间(a,a+1)内存在极值点,则实数a的取值范围是( )
| A. | (-3,-1)∪(0,2) | B. | (-3,-2)∪(-1,0) | C. | (-2,-1)∪(0,3) | D. | (-3,-2)∪(0,1) |
11.已知关于x的方程x2-2ax+2a2-3a+2=0有两个不等的实数根x1,x2,那么(x1-x2)2的取值范围是( )
| A. | (0,+∞) | B. | [0,1] | C. | (0,1] | D. | (0,1) |