题目内容
函数f（x）=2x2-lnx的单调递增区间为
- A.
- B.
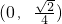
- C.
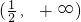
- D.
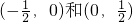
C
分析：先计算函数的导函数f′（x），再解不等式f′（x）＞0即可得函数的单调增区间，注意函数的定义域为（0，+∞）
解答：依题意，f′（x）=4x-
=
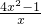（x＞0）
由f′（x）＞0，得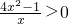
?4x2-1＞0?x＞
∴函数f（x）=2x2-lnx的单调递增区间为[，+∞）
故选C
点评：本题考察了利用导数求函数单调区间的方法，解题时要特别注意函数的定义域，能熟练的求导和解简单的不等式
分析：先计算函数的导函数f′（x），再解不等式f′（x）＞0即可得函数的单调增区间，注意函数的定义域为（0，+∞）
解答：依题意，f′（x）=4x-
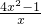= （x＞0）由f′（x）＞0，得
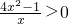?4x2-1＞0?x＞∴函数f（x）=2x2-lnx的单调递增区间为[
，+∞）故选C
点评：本题考察了利用导数求函数单调区间的方法，解题时要特别注意函数的定义域，能熟练的求导和解简单的不等式
练习册系列答案
相关题目
函数f（x）=2x2-6x+1在区间[-1，1]上的最小值为（ ）
| A、9 | ||
| B、-3 | ||
C、
| ||
D、
|