题目内容
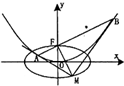 已知抛物线C:x2=4y的焦点为F,过点F作直线l交抛物线C于A、B两点;椭圆E的中心在原点,焦点在x轴上,点F是它的一个顶点,且其离心率e=
已知抛物线C:x2=4y的焦点为F,过点F作直线l交抛物线C于A、B两点;椭圆E的中心在原点,焦点在x轴上,点F是它的一个顶点,且其离心率e=
| ||
| 2 |
(1)经过A、B两点分别作抛物线C的切线l1,l2,切线l1与l2相交于点M.证明:
| MF |
| MA |
| MF |
| MB |
(2)椭圆E上是否存在一点M',经过点M'作抛物线C的两条切线M'A',M'B'(A',B'为切点),使得直线A'B'过点F?若存在,求出抛物线C与切线M'A',M'B'所围成图形的面积;若不存在,请说明理由.
分析:(1)联立
,得x2-4kx-4=0,x1+x2=4k,x1x2=-4,由抛物线C的方程为y=
x2,知y′=
x,过抛物线上A、B两点的切线方程分别是y-y1=
x1(x-x1),y-y2=
x2(x-x2),由此能够求
•
=
•
.
(2)设椭圆E的方程为
+
=1(a+b>0),半焦距为c,
,解得a=2,b=1,所以椭圆E的方程是
+y2 =1.假设存在点M‘满足题意,点M’心在直线y=-1上,由此能够求出抛物线C与切线M′A′,M′B′所围成图形的面积是S=2
[
x2-(x-1)] dx=
(
x3-
x2+x)
=
.
|
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| FM |
| MA |
| MF |
| MB |
(2)设椭圆E的方程为
| x2 |
| a2 |
| y2 |
| b2 |
|
| x2 |
| 4 |
| ∫ | 2 0 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 12 |
| 1 |
| 2 |
| | | 2 0 |
| 4 |
| 3 |
解答:解:(1)联立
,得x2-4kx-4=0,
∴x1+x2=4k,x1x2=-4,
∵抛物线C的方程为y=
x2,∴y′=
x,
∴过抛物线上A、B两点的切线方程分别是
y-y1=
x1(x-x1),y-y2=
x2(x-x2),
即y=
x1 x-
x12,y=
x2x-
x22,
解得两条切线l1,l2的交点坐标为(
,
),即M(2k,-1),
要证
•
=
•
,即证
•(
-
) =
•
=0,
∵
•
=(2k,-2)•(x2-x1,y2-y1)
=2k(x2-x1)-
=0,∴
•
=
•
.
(2)设椭圆E的方程为
+
=1(a+b>0),半焦距为c,
,解得a=2,b=1,
∴椭圆E的方程是
+y2 =1.
假设存在点M‘满足题意,由(1)知,点M’心在直线y=-1上,
又直线y=-1与椭圆E有唯一交点,故M‘(0,-1).
设过点M’且与抛物线C相切的切线方程这:y-y0=
x0(x-x0),
其中点(x0,y0)为切点,
令x=0,y=-1,得-1-
x02=
x0(0-x0),
解得x0=2或x0=-2.
取A‘(-2,1),B’(2,1)即直线A‘B’过点F,
综上所述,椭圆E上存在一点M‘(0,-1),经过点M′作抛物线C的两条切线M′A′,M′B′(A′,B′为切点),
此时,两条切线分别为y=-x-1,y=x-1.
抛物线C与切线M′A′,M′B′所围成图形的面积是S=2
[
x2-(x-1)] dx=
(
x3-
x2+x)
=
.
|
∴x1+x2=4k,x1x2=-4,
∵抛物线C的方程为y=
| 1 |
| 4 |
| 1 |
| 2 |
∴过抛物线上A、B两点的切线方程分别是
y-y1=
| 1 |
| 2 |
| 1 |
| 2 |
即y=
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
解得两条切线l1,l2的交点坐标为(
| x1+x2 |
| 2 |
| x1x2 |
| 4 |
要证
| MF |
| MA |
| MF |
| MB |
| MF |
| MB |
| MA |
| MF |
| AB |
∵
| FM |
| AB |
=2k(x2-x1)-
| (x2+x1)(x2-x2) |
| 2 |
| FM |
| MA |
| MF |
| MB |
(2)设椭圆E的方程为
| x2 |
| a2 |
| y2 |
| b2 |
|
∴椭圆E的方程是
| x2 |
| 4 |
假设存在点M‘满足题意,由(1)知,点M’心在直线y=-1上,
又直线y=-1与椭圆E有唯一交点,故M‘(0,-1).
设过点M’且与抛物线C相切的切线方程这:y-y0=
| 1 |
| 2 |
其中点(x0,y0)为切点,
令x=0,y=-1,得-1-
| 1 |
| 4 |
| 1 |
| 2 |
解得x0=2或x0=-2.
取A‘(-2,1),B’(2,1)即直线A‘B’过点F,
综上所述,椭圆E上存在一点M‘(0,-1),经过点M′作抛物线C的两条切线M′A′,M′B′(A′,B′为切点),
此时,两条切线分别为y=-x-1,y=x-1.
抛物线C与切线M′A′,M′B′所围成图形的面积是S=2
| ∫ | 2 0 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 12 |
| 1 |
| 2 |
| | | 2 0 |
| 4 |
| 3 |
点评:本题考查直线和圆锥曲线的位置关系的综合运用,解题时要认真审题,仔细解答,注意合理地进行等价转化.

练习册系列答案
相关题目