题目内容
已知抛物线C:x2=2my(m>0)和直线l:y=x-m没有公共点(其中m为常数).动点P是直线l上的任意一点,过P点引抛物线C的两条切线,切点分别为M、N,且直线MN恒过点Q(1,1).
(1)求抛物线C的方程;
(2)已知O点为原点,连接PQ交抛物线C于A、B两点,求
-
的值.
(1)求抛物线C的方程;
(2)已知O点为原点,连接PQ交抛物线C于A、B两点,求
| ||
|
|
|
| ||
|
|
分析:(1)对C的函数求导数,设出两个切点的坐标,求出导函数在切点处的导数值即切线的斜率,利用点斜式写出切线
PM,PN 的方程,将P的坐标代入得到MN的方程,据直线的点斜式判断出MN过的定点,据已知求出抛物线C的方程.
(2)设出直线PQ的方程,将直线方程与抛物线方程联立,利用韦达定理得解.
PM,PN 的方程,将P的坐标代入得到MN的方程,据直线的点斜式判断出MN过的定点,据已知求出抛物线C的方程.
(2)设出直线PQ的方程,将直线方程与抛物线方程联立,利用韦达定理得解.
解答:解:(1)如图,设M(x1,y1),N(x2,y2)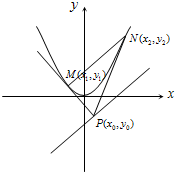
由y=
,得y′=
,∴PM的斜率为
,PM的方程为y=
x-y1
同理得PN:y=
x-y2,
设P(x0,y0)代入上式得 y0=
x0-y1,y0=
x0-y2,
即(x1,y1),(x2,y2)满足方程y0=
x0-y
故MN的方程为y=
x-y0=
x-(x0-m)
上式可化为y-m=
(x-m),过交点(m,m)
∵MN过交点Q(1,1),
∴m=1
∴抛物线C的方程为x2=2y
(2)设A(x3,y3),B(x4,y4)
则
-
=
…(Ⅰ)
∵P(x0,y0),Q(1,1)
∴PQ直线方程为y-1=
(x-1),
与x2=2y联立化简x2-
x+
-2=0
∴x3x4=
…①,x3+x4=
…②
把①②代入(Ⅰ)式中,
则分子2x3x4-(1+x0)(x3+x4)+2kx0=
…(Ⅱ)
又P点在直线y=kx-1上,
∴y0=kx0-1代入(Ⅱ)中得:2x3x4-(1+x0)(x3+x4)+2kx0=0
∴
-
=
=0
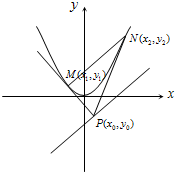
由y=
| x2 |
| 2m |
| x |
| m |
| x1 |
| m |
| x1 |
| m |
同理得PN:y=
| x2 |
| m |
设P(x0,y0)代入上式得 y0=
| x1 |
| m |
| x2 |
| m |
即(x1,y1),(x2,y2)满足方程y0=
| x |
| m |
故MN的方程为y=
| x0 |
| m |
| x0 |
| m |
上式可化为y-m=
| x0 |
| m |
∵MN过交点Q(1,1),
∴m=1
∴抛物线C的方程为x2=2y
(2)设A(x3,y3),B(x4,y4)
则
| ||
|
|
|
| ||
|
|
| 2x3x4-(1+x0)(x3+x4)+2kx0 |
| (x4-x0)(x4-1) |
∵P(x0,y0),Q(1,1)
∴PQ直线方程为y-1=
| y0-1 |
| x0-1 |
与x2=2y联立化简x2-
| 2y0-2 |
| x0-1 |
| 2y0-2 |
| x0-1 |
∴x3x4=
| 2y0-2x0 |
| x0-1 |
| 2y0-2 |
| x0-1 |
把①②代入(Ⅰ)式中,
则分子2x3x4-(1+x0)(x3+x4)+2kx0=
4y0-2(y0-1)(1+x0)
| ||
| x0-1 |
又P点在直线y=kx-1上,
∴y0=kx0-1代入(Ⅱ)中得:2x3x4-(1+x0)(x3+x4)+2kx0=0
∴
| ||
|
|
|
| ||
|
|
| 2x3x4-(1+x0)(x3+x4)+2kx0 |
| (x4-x0)(x4-1) |
点评:解决直线与圆锥曲线的位置关系问题,一般是设出直线方程,将直线方程与圆锥曲线方程联立,消去一个未知数,得到关于一个未知数的二次方程,然后利用韦达定理找突破口.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案
相关题目