题目内容
【题目】设
为奇函数，
为常数．
（1）求证：
是
上的增函数；
（2）若对于区间
上的每一个
值，不等式
恒成立，求实数
取值范围．
【答案】（1）证明见解析；（2）
【解析】
（1）由奇函数的定义域关于原点对称可得，
，即
，则令
，得到的根必为相反数，从而求出a，再根据定义法证明
是
上的增函数即可；
（2）由题意知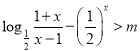
，
时恒成立，令
，根据单调性的运算可判断
的单调性，从而求出最值.
（1）∵是奇函数，∴定义域关于原点对称，
由，得．令，得
，
，
∴
，解得
，
，令
，
设任意
，且
，则
，
∵
，∴
，
，
，∴
，即
．
∴
是减函数，又
为减函数，
∴在上为增函数；
（2）由题意知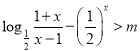，时恒成立，
令，，
由（2）知
在
上为增函数，又
在
上也是增函数，
故在上为增函数，∴的最小值为
，
∴
，故实数
的范围是．
练习册系列答案
举一反三同步巧讲精练系列答案
口算与应用题卡系列答案
相关题目
【题目】某协会对
，
两家服务机构进行满意度调查，在，两家服务机构提供过服务的市民中随机抽取了
人，每人分别对这两家服务机构进行独立评分，满分均为
分.整理评分数据，将分数以
为组距分成
组：
，
，
，
，
，
，得到服务机构分数的频数分布表，服务机构分数的频率分布直方图：
定义市民对服务机构评价的“满意度指数”如下：
分数 |
|
|
|
满意度指数 | 0 | 1 | 2 |
（1）在抽样的人中，求对服务机构评价“满意度指数”为
的人数；
（2）从在，两家服务机构都提供过服务的市民中随机抽取
人进行调查，试估计对服务机构评价的“满意度指数”比对服务机构评价的“满意度指数”高的概率；
（3）如果从，服务机构中选择一家服务机构，以满意度出发，你会选择哪一家？说明理由.
